Пошаговое объяснение:
для исследования функции понадобятся первая и вторая производные. я их сразу найду, чтобы потом не повторяться
теперь поехали
1. Область определения D(y) и область допустимых значений E(y) функции.
D(y)= (x∈ R ; x≠ 0)
E(y) = ( y∈ R ; y ≥0)
2 Четность, нечетность функции.
эта функция не является четной и не является нечетной
четность y(-x) = y(x) смотрим
нечетность y(-x) = -y(x) смотрим
3.Точки пересечения с осями. или так называемые нули функции
y' = 0; ⇒ x₀ = 1 y(1)=0; точка пересечения с осью ОХ К(1;0)
4.Асимптоты функции
ищем в виде y = ax +b
из определения асимптоты
найдем к и b
мы получили горизонтальную асимптоту у = 1
теперь вртикальная асимптота
точка разрыва у нас х₀ = 0
посмотрим, какого она рода и является ли х = 0 асимптотой
x= 0 есть вертикальная асимптота
5.Экстремумы и интервалы монотонности.
критические точки, (они же точки экстремума, они же потенциальные точки смены знака) ищутся y' = 0
⇒ x₁ = 1 - точка экстремума.
используем вторую производную, чтобы определить точка минимума или точка максимума
y''(1)=2 > 0 значит точка x₁ = 1 точка минимума функции.
к этой точке добавим точку разрыва х₀ = 0
и вот мы получили интервалы возрастания и убывания функции
смотрим знак производной на интервале. берем любую точку ∈ интервалу и вычисляем значение производной
(-∞; 0) y'(-1) = 4 > 0 - функция возрастает
(0; 1) y'(0,5) = -8 < 0 - функция убывает
(1; +∞) y'(2) = 0.25 > 0 - функция возрастает
6.Точки перегиба и промежутки выпуклости, вогнутости.
⇒ x₁ = 1.5 точка перегиба
к этой точке добавим точку разрыва x₀ = 0 - потенциальную точку перегиба
и вот мы получили интервалы перегибов функции
(-∞; 0) y''(-1) = 10 > 0 - функция вогнута
(0; 1,5) y''(1) = 2 > 0 - функция вогнута
(1.5; +∞) y''(2) = -0.25 < 0 - функция выпукла
x₁ = 1.5 -да, а вот x₁ = 1.5 нет тогда у(1,5) = 1/9
т.о точка прегиба M(3/2; 1/9)
(попытался показать как она выглядит через местную вставку уравнений, без понятия если будет работать как надо)
Пошаговое объяснение:
для исследования функции понадобятся первая и вторая производные. я их сразу найду, чтобы потом не повторяться
теперь поехали
1. Область определения D(y) и область допустимых значений E(y) функции.
D(y)= (x∈ R ; x≠ 0)
E(y) = ( y∈ R ; y ≥0)
2 Четность, нечетность функции.
эта функция не является четной и не является нечетной
четность y(-x) = y(x) смотрим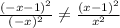
нечетность y(-x) = -y(x) смотрим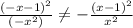
3.Точки пересечения с осями. или так называемые нули функции
y' = 0;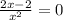
⇒ x₀ = 1 y(1)=0; точка пересечения с осью ОХ К(1;0)
4.Асимптоты функции
ищем в виде y = ax +b
из определения асимптоты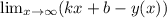
найдем к и b
мы получили горизонтальную асимптоту у = 1
теперь вртикальная асимптота
точка разрыва у нас х₀ = 0
посмотрим, какого она рода и является ли х = 0 асимптотой
x= 0 есть вертикальная асимптота
5.Экстремумы и интервалы монотонности.
критические точки, (они же точки экстремума, они же потенциальные точки смены знака) ищутся y' = 0
используем вторую производную, чтобы определить точка минимума или точка максимума
к этой точке добавим точку разрыва х₀ = 0
и вот мы получили интервалы возрастания и убывания функции
смотрим знак производной на интервале. берем любую точку ∈ интервалу и вычисляем значение производной
(-∞; 0) y'(-1) = 4 > 0 - функция возрастает
(0; 1) y'(0,5) = -8 < 0 - функция убывает
(1; +∞) y'(2) = 0.25 > 0 - функция возрастает
6.Точки перегиба и промежутки выпуклости, вогнутости.
к этой точке добавим точку разрыва x₀ = 0 - потенциальную точку перегиба
и вот мы получили интервалы перегибов функции
(-∞; 0) y''(-1) = 10 > 0 - функция вогнута
(0; 1,5) y''(1) = 2 > 0 - функция вогнута
(1.5; +∞) y''(2) = -0.25 < 0 - функция выпукла
x₁ = 1.5 -да, а вот x₁ = 1.5 нет тогда у(1,5) = 1/9
т.о точка прегиба M(3/2; 1/9)