Сходится
Пошаговое объяснение:
Особая точка .
Подынтегральная функция представима в виде , где .
1) непрерывна на .
2)
3) непрерывна на . При этом , а значит монотонно убывает.
4)
Значит, интеграл сходится по признаку Дирихле.
Сходится
Пошаговое объяснение:
Особая точка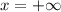 .
.
Подынтегральная функция представима в виде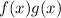 , где
, где 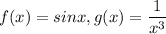 .
.
1)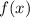 непрерывна на
непрерывна на 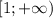 .
.
2)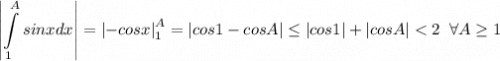
3)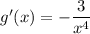 непрерывна на
непрерывна на 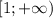 . При этом
. При этом 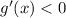 , а значит
, а значит 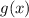 монотонно убывает.
монотонно убывает.
4)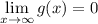
Значит, интеграл сходится по признаку Дирихле.