Сходится
Пошаговое объяснение:
, .
Пусть . При этом .
.
Тогда, так как и ряд сходится, то, по предельному признаку сравнения, ряд также сходится.
Сходится
Пошаговое объяснение:
Пусть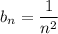 . При этом
. При этом 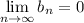 .
.
Тогда, так как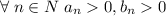 и ряд
и ряд 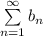 сходится, то, по предельному признаку сравнения, ряд
сходится, то, по предельному признаку сравнения, ряд 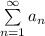 также сходится.
также сходится.