Из города N в город М выехал автомобиль со скоростью 50 км/час. Через 1 час в том же направлении выехал 2-й автомобиль со скоростью 60 км/час. Еще через 1 час выехал 3-й автомобиль. Какова скорость 3-го автомобиля, если через некоторое время 2-й и 3-й автомобили догнали 1-й автомобиль?
Раз некоторое число удовлетворяет уравнению при любом
удовлетворяет уравнению при любом  , то оно также удовлетворяет уравнению при
, то оно также удовлетворяет уравнению при 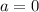 .
.
То есть, если мы подставим в уравнение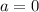 , то выполнится равенство:
, то выполнится равенство:
Оба корня удовлетворяют уравнению и ОДЗ (при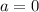 ): с обеих сторон в первом случае получается
): с обеих сторон в первом случае получается  , а во втором
, а во втором 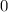 (так как мы не выписывали ОДЗ, то мы могли получить "лишние корни", но мы их не получили).
(так как мы не выписывали ОДЗ, то мы могли получить "лишние корни", но мы их не получили).
Очевидно, что эти два корня в ответ так сразу не пойдут. Мы знаем лишь только, что они подходят при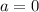 . И если ответ на задачу существует, то он может быть только
. И если ответ на задачу существует, то он может быть только 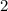 ,
, 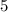 или и
или и 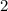 , и
, и 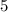 . Но про другие значения
. Но про другие значения  мы пока ничего не знаем.
мы пока ничего не знаем.
Посмотрим, что у нас будет получаться при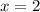 :
:
Вот только первый логарифм не всегда существует.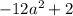 может быть отрицательным (возьмите, к примеру,
может быть отрицательным (возьмите, к примеру, 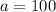 ). А подлогарифмическое выражение обязано быть положительным. Значит, такой
). А подлогарифмическое выражение обязано быть положительным. Значит, такой  нас не устраивает.
нас не устраивает.
Теперь проверим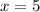 :
:
В обеих частях мы получили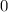 (так как
(так как 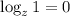 , если
, если 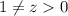 ). Также
). Также 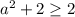 , поэтому все ограничения будут выполняться.
, поэтому все ограничения будут выполняться.
В итоге имеем нужный ответ: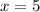 .
.
Задача решена!
12 = 2 • 2 • 3
Разложим на простые множители 20
20 = 2 • 2 • 5
Выберем одинаковые простые множители в обоих числах.
2 , 2
Находим произведение одинаковых простых множителей и записываем ответ
НОД (12; 20) = 2 • 2 = 4
Разложим на простые множители 27
27 = 3 • 3 • 3
Разложим на простые множители 72
72 = 2 • 2 • 2 • 3 • 3
Выберем одинаковые простые множители в обоих числах.
3 , 3
Находим произведение одинаковых простых множителей и записываем ответ
НОД (27; 72) = 3 • 3 = 9
Разложим на простые множители 60
60 = 2 • 2 • 3 • 5
Разложим на простые множители 64
64 = 2 • 2 • 2 • 2 • 2 • 2
Выберем одинаковые простые множители в обоих числах.
2 , 2
Находим произведение одинаковых простых множителей и записываем ответ
НОД (60; 64) = 2 • 2 = 4
Разложим на простые множители 36
36 = 2 • 2 • 3 • 3
Разложим на простые множители 96
96 = 2 • 2 • 2 • 2 • 2 • 3
Выберем одинаковые простые множители в обоих числах.
2 , 2 , 3
Находим произведение одинаковых простых множителей и записываем ответ
НОД (36; 96) = 2 • 2 • 3 = 12
Разложим на простые множители 360
360 = 2 • 2 • 2 • 3 • 3 • 5
Разложим на простые множители 840
840 = 2 • 2 • 2 • 3 • 5 • 7
Выберем одинаковые простые множители в обоих числах.
2 , 2 , 2 , 3 , 5
Находим произведение одинаковых простых множителей и записываем ответ
НОД (360; 840) = 2 • 2 • 2 • 3 • 5 = 120
Разложим на простые множители 84
84 = 2 • 2 • 3 • 7
Разложим на простые множители 112
112 = 2 • 2 • 2 • 2 • 7
Выберем одинаковые простые множители в обоих числах.
2 , 2 , 7
Находим произведение одинаковых простых множителей и записываем ответ
НОД (84; 112) = 2 • 2 • 7 = 28