Случайная величина X - число вынутых белых шаров.
Опыт может быть проведен один раз, если черный шар появится сразу:
Если же в первый раз извлекли белый шар, а при втором извлечении появился черный шар, то
Если же при втором извлечении появился белый шар, а и при третьем черный шар, то
Аналогично
Xi 0 1 2 3
Pi 11/12 11/140 11/2380 1/7140
Случайная величина Х распределена дискретно
Математическое ожидание дискретной случайной величины X:
Случайная величина X - число вынутых белых шаров.
Опыт может быть проведен один раз, если черный шар появится сразу: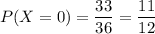
Если же в первый раз извлекли белый шар, а при втором извлечении появился черный шар, то
Если же при втором извлечении появился белый шар, а и при третьем черный шар, то
Аналогично
Xi 0 1 2 3
Pi 11/12 11/140 11/2380 1/7140
Случайная величина Х распределена дискретно
Математическое ожидание дискретной случайной величины X: