Запишем одз: так как 2>0 то достаточно чтобы x≠1 и х>0 Так же logx(2)=1/log2(x) Перепишем так систему (фигурная скобка):01, после возведения 2 в эту степень выйдет х>2(знаки сохраняются потому что 2^x больше если больше степень (если число между 0 и 1 то знаки пришлось бы менять но мы возводим 2 в степень)) Logx(2)<=-1 перепишем так -1<=log2(x)<0(если число меньше минус 1 то обратное между -1 и 0 а если число -1 то обратное -1) возводим 2 в эту степень 2^-1<=х<2^0(знаки сохраняются об этом уже говорилось) тогда 1/2<=х<1 Выходит объединение [1/2;1) и (2;+бесконечность) ответ объединение [1/2;1) и (2;+бесконечность)
Так же logx(2)=1/log2(x)
Перепишем так систему (фигурная скобка):01, после возведения 2 в эту степень выйдет х>2(знаки сохраняются потому что 2^x больше если больше степень (если число между 0 и 1 то знаки пришлось бы менять но мы возводим 2 в степень))
Logx(2)<=-1 перепишем так -1<=log2(x)<0(если число меньше минус 1 то обратное между -1 и 0 а если число -1 то обратное -1) возводим 2 в эту степень 2^-1<=х<2^0(знаки сохраняются об этом уже говорилось) тогда 1/2<=х<1
Выходит объединение [1/2;1) и (2;+бесконечность)
ответ объединение [1/2;1) и (2;+бесконечность)
49 см²
Пошаговое объяснение:
Вариант 1
Площадь прямоугольника - 14*7=98см²
Площадь прямоугольного треугольника считается по формуле =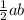
где a и b - катеты.
Катеты треугольников ABS и CDU равны 7 и 7 см (точки S и U - середина, значит катеты CU и AS равны 7 см).
Отсюда площадь треугольника =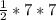
= 24.5 см²
Площадь двух треугольников = 24.5*2=49 см²
Значит площадь заштрихованной фигуры = 98-49=49 см²
Вариант 2 (в качестве альтернативного решения)
т.к. точки U и S - середина, то образуются квадратыUCDS и BUSA со стороной 7 см. Т.к. треугольники занимают ровно половину квадратов, то получаем:
площадь квадрата - 7*7=49см²
из них заштрихованная = 49/2=24,5см²
Площадь двух заштрихованных областей - 24,5*2=49см²