Пусть сумма кредита равна S, а годовые составляют а %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент: b = 1 + 0,01a. После первой выплаты сумма долга составит: S1 = Sb − X. После второй выплаты сумма долга составит: S2 = S1b − X = (Sb − X)b − X = Sb² − (1 + b)X. После третьей выплаты сумма оставшегося долга равна: S3 = Sb³ - (1-b+b²)X = Sb³ - · X После четвертой выплаты сумма оставшегося долга равна: S4 = - (1 + b +b² + b³)X = - · X По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому - · X = 0. Потом выражаешь из этого выражения X и при S = 6902000 и а = 12,5, получаем: b = 1,125 получается: X = рублей
Пишем вероятности событий p1 = 0.7 q1 = 1-0.7=0.3 p2 = 0.8 q2 = 0.2 А теперь разные события по условию задачи. Событие А - сдаст И 1-1 И 2-й - Р(А) =p1*p2 = 0.7*0.8 = 0.56 = 56% - ОТВЕТ Событие Б - не сдаст И 1-й И 2-й - Р(Б) = q1*q2 = 0.3*0.2= 0.06 = 6% - ОТВЕТ Событие В - сдаст ТОЛЬКО один - Р(В) = p1*q2 + q1*p2 =0.7*0.2+0.8*0.3 = =0,14+0,24 = 0,38 = 38% - ОТВЕТ Событие Г - сдаст ХОТЯ бы один - ИЛИ 1-й ИЛИ 2-й ИЛИ оба. Р(Г) = p1*q2+ q1*p2 + p1*p2 = 0.7*0.2+0.3*0.8+0.7*0.8 = 0.14+0.24+0.56=94% - ОТВЕТ или Можно рассчитать как обратное событию Б Р(Г)= 1 - Р(Б) = 1-0,06=0,94
Пусть сумма кредита равна S, а годовые составляют а %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент: b = 1 + 0,01a.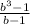 · X
· X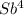 - (1 + b +b² + b³)X =
- (1 + b +b² + b³)X = 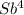 -
- 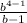 · X
· X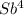 -
- 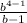 · X = 0.
· X = 0.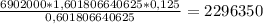 рублей
рублей
После первой выплаты сумма долга составит:
S1 = Sb − X.
После второй выплаты сумма долга составит:
S2 = S1b − X = (Sb − X)b − X = Sb² − (1 + b)X.
После третьей выплаты сумма оставшегося долга равна:
S3 = Sb³ - (1-b+b²)X = Sb³ -
После четвертой выплаты сумма оставшегося долга равна:
S4 =
По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому
Потом выражаешь из этого выражения X и при S = 6902000 и а = 12,5, получаем: b = 1,125 получается:
X =
p1 = 0.7 q1 = 1-0.7=0.3
p2 = 0.8 q2 = 0.2
А теперь разные события по условию задачи.
Событие А - сдаст И 1-1 И 2-й - Р(А) =p1*p2 = 0.7*0.8 = 0.56 = 56% - ОТВЕТ
Событие Б - не сдаст И 1-й И 2-й - Р(Б) = q1*q2 = 0.3*0.2= 0.06 = 6% - ОТВЕТ
Событие В - сдаст ТОЛЬКО один - Р(В) = p1*q2 + q1*p2 =0.7*0.2+0.8*0.3 =
=0,14+0,24 = 0,38 = 38% - ОТВЕТ
Событие Г - сдаст ХОТЯ бы один - ИЛИ 1-й ИЛИ 2-й ИЛИ оба.
Р(Г) = p1*q2+ q1*p2 + p1*p2 = 0.7*0.2+0.3*0.8+0.7*0.8 = 0.14+0.24+0.56=94% - ОТВЕТ или
Можно рассчитать как обратное событию Б Р(Г)= 1 - Р(Б) = 1-0,06=0,94