Пояснения:
Для решения задания можно применить рациональное свойство деления относительно сложения и вычитания:
(а + в) : с = а : с + в : с
(а - в) : с = а : с - в : с
Для этого надо разбить делимое на части, которые можно разделить на предложенный делитель "в уме", а потом сложить( вычесть) полученные частные.
225 : 9 = (180 + 45) : 9 = 180 : 9 + 45 : 9 = 20 + 5 = 25 или:
225 : 9 = (270 - 45) : 9 = 270 : 9 - 45 : 9 = 30 - 5 = 25
840 : 24 = (960 - 120) : 24 = 960 : 24 - 120 : 24 = 40 - 5 = 35 или:
840 : 24 = (720 + 120) : 24 = 720 : 24 + 120 : 24 = 30 + 5 = 35
А — из случайно отобранных 4 телевизора все хорошие;
В — два хорошие и два нет;
С — один хороший и три нет;
D — хороших нет.
Общее число элементарных исходов равно числу выбрать 4 телевизоров из 16. Т.е.
1) Найдем вероятность события А.
Число благоприятных исходов: выбрать 4 хороших телевизора из 11 можно
Искомая вероятность:
2) Вероятность события В:
Число благоприятных исходов: выбрать два хороших телевизора можно а два НЕ хороших телевизора можно . По правилу произведения, всего таких
3) Вероятность события C:
Выбрать один хороший телевизор можно Выбрать три НЕ хороших телевизора можно По правилу произведения, таких
4) Вероятность события D
Выбрать четыре НЕ хороших телевизора можно
Пояснения:
Для решения задания можно применить рациональное свойство деления относительно сложения и вычитания:
(а + в) : с = а : с + в : с
(а - в) : с = а : с - в : с
Для этого надо разбить делимое на части, которые можно разделить на предложенный делитель "в уме", а потом сложить( вычесть) полученные частные.
225 : 9 = (180 + 45) : 9 = 180 : 9 + 45 : 9 = 20 + 5 = 25 или:
225 : 9 = (270 - 45) : 9 = 270 : 9 - 45 : 9 = 30 - 5 = 25
840 : 24 = (960 - 120) : 24 = 960 : 24 - 120 : 24 = 40 - 5 = 35 или:
840 : 24 = (720 + 120) : 24 = 720 : 24 + 120 : 24 = 30 + 5 = 35
А — из случайно отобранных 4 телевизора все хорошие;
В — два хорошие и два нет;
С — один хороший и три нет;
D — хороших нет.
Общее число элементарных исходов равно числу выбрать 4 телевизоров из 16. Т.е.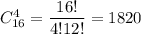
1) Найдем вероятность события А.
Число благоприятных исходов: выбрать 4 хороших телевизора из 11 можно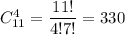
Искомая вероятность:
2) Вероятность события В:
Число благоприятных исходов: выбрать два хороших телевизора можно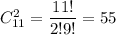 а два НЕ хороших телевизора можно
а два НЕ хороших телевизора можно 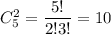 . По правилу произведения, всего таких
. По правилу произведения, всего таких 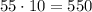
Искомая вероятность:
3) Вероятность события C:
Выбрать один хороший телевизор можно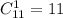 Выбрать три НЕ хороших телевизора можно
Выбрать три НЕ хороших телевизора можно 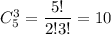 По правилу произведения, таких
По правилу произведения, таких 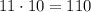
Искомая вероятность:
4) Вероятность события D
Выбрать четыре НЕ хороших телевизора можно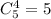
Искомая вероятность: