1) А(60; 4): Поезд ехал в течении 4 часов со скоростью 60 км/час.
2) час
Пошаговое объяснение:
1) Проекция координату точки А на ось скорости - это 60, а проекция координату точки А на ось времени - это 4: А(60; 4). Это означает, что в течении 4 часов поезд ехал со скоростью 60 км/час.
2) Формула зависимости времени движения (t) поезда от его скорости (υ) при постоянном расстоянии имеет вид:
час
Проверим формулу в некоторых целых координатных точках:
Поскольку при выкладывании по 8 и по 9 плиток в ряд прямоугольников не получается, а остаются неполные ряды, то количество плиток делится на 8 и на 9 с остатками.
Остаток от деления любого числа на 8 не может быть больше 7. По условию это число на 6 больше, чем остаток от деления на 9. Но остаток от деления на 9 тоже не равен нулю. Значит, остаток от деления на 8 может быть равен только 7. А остаток от деления на 9 равен 1.
Общее количество плиток меньше 100, иначе их хватило бы на квадратную площадку со стороной в 10 плиток. Среди чисел меньше 100 надо найти такое, которое делится на 8 с остатком 7 и на 9 с остатком 1. Проверив все числа в пределах 100, делящиеся на 9 с остатком 1, получим ответ: 55 плиток.
1) А(60; 4): Поезд ехал в течении 4 часов со скоростью 60 км/час.
2)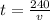 час
час
Пошаговое объяснение:
1) Проекция координату точки А на ось скорости - это 60, а проекция координату точки А на ось времени - это 4: А(60; 4). Это означает, что в течении 4 часов поезд ехал со скоростью 60 км/час.
2) Формула зависимости времени движения (t) поезда от его скорости (υ) при постоянном расстоянии имеет вид:
Проверим формулу в некоторых целых координатных точках:
υ=30 км/час ---> t = 8 часов
υ=40 км/час ---> t = 6 часов
υ=60 км/час ---> t = 4 часа
υ=80 км/час ---> t = 3 часа
υ=120 км/час ---> t = 2 часа
Поскольку при выкладывании по 8 и по 9 плиток в ряд прямоугольников не получается, а остаются неполные ряды, то количество плиток делится на 8 и на 9 с остатками.
Остаток от деления любого числа на 8 не может быть больше 7. По условию это число на 6 больше, чем остаток от деления на 9. Но остаток от деления на 9 тоже не равен нулю. Значит, остаток от деления на 8 может быть равен только 7. А остаток от деления на 9 равен 1.
Общее количество плиток меньше 100, иначе их хватило бы на квадратную площадку со стороной в 10 плиток. Среди чисел меньше 100 надо найти такое, которое делится на 8 с остатком 7 и на 9 с остатком 1. Проверив все числа в пределах 100, делящиеся на 9 с остатком 1, получим ответ: 55 плиток.
Пошаговое объяснение: