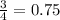Как продемонстрировать периметр треугольника? инструкция (какие действия необходимо выполнить, чтобы продемонстрировать выбранное утверждение): 1 шаг: 2 шаг:
Сравним: 1 ) 20 км 010 м и 20 100 м ; 20 * 1 км + 010 м и 20 100 м ; 20 * 1000 м + 010 м и 20 100 м ; 20 000 + 010 м и 20 100 м ; 20 010 м < 20 100 м ; Значит, 20 км 010 м < 20 100 м ; 2 ) 54 т 740 кг и 5 474 ц ; 54 000 кг + 740 кг = 5 474 * 100 кг ; 54 740 кг < 547 400 кг ; Значит, 54 т 740 кг < 5 474 ц ; 3 ) 19 дм 5 см и 1 950 мм ; 19 * 10 см + 5 см и 1 950 мм ; 195 см и 1 950 мм : 1950 мм = 1 950 мм; 4 ) 3 т 2 ц и 3 200 кг ; 3 000 кг + 200 кг и 3 200 кг ; 3 200 кг = 3 200 кг ; 5 ) 8 м 1 дм и 810 дм ; 8 * 10 дм + 1 дм и 810 дм ; 81 дм < 810 дм ; 6 ) 106 ц 75 кг и 67 500 г ; 10 600 кг + 75 кг и 67 500 г ; 10 675 кг > 67 500 г.
В принципе, решение можно осуществить 2 путями. Для начала, обозначим вероятности
Pн - нечетное произведение очков,
Рч - четное произведение очков
1. При двух бросках в результате могут быть только 2 вероятных события:
- четное произведение очков
- нечетное произведение очков.
Эти 2 случая охватывают полностью возможные наступления событий.
Соответственно, верно равенство
Произведение 2 чисел будет НЕчетным тогда, когда НЕчетными являются ОДНОВРЕМЕННО ОБА из множителей.
Два броска являются независимыми (результат 2 броска не зависит от числа, выпавшего первым);
Из равновероятных 6 событий для одного броска нечетныеэми будут 3.
Следовательно, вероятность нечетного броска равна
Вероятность того, что произведение чисел бросков будет нечетным равна вероятности двойного нечетного броска - т.е. произведению вероятностей для 1 и 2 броска:
Следовательно, вероятность того, что произведение чисел бросков будет четным равна разности между 1 и Рн:
2. Возможны варианты бросков (первый-второй броски):
1 - чч - четный-четный
2 - чн - четный-нечетный
3 - нч - нечетный-четный
4 - нн - нечетный-нечетный.
Произведение же четно, когда четным является ХОТЯ БЫ ОДИН из множителей.
А это происходит в трех случаях из 4-х - случае 1, 2 и 3 из указанных выше.
То есть
Легко проверить, что вероятность наступления каждого из событий равна:
произведению вероятности четности/нечетности первого броска на вероятность четности/нечетности второго броска.
Для любого броска вероятность четного числа очков равна вероятности нечетного и составляет
Следовательно:
А значит,
Итак, в двух различных решениях получили одинаковые результаты. Следовательно, ответ верен:
Пошаговое объяснение:
В принципе, решение можно осуществить 2 путями. Для начала, обозначим вероятности
Pн - нечетное произведение очков,
Рч - четное произведение очков
1. При двух бросках в результате могут быть только 2 вероятных события:
- четное произведение очков
- нечетное произведение очков.
Эти 2 случая охватывают полностью возможные наступления событий.
Соответственно, верно равенство
Произведение 2 чисел будет НЕчетным тогда, когда НЕчетными являются ОДНОВРЕМЕННО ОБА из множителей.
Два броска являются независимыми (результат 2 броска не зависит от числа, выпавшего первым);
Из равновероятных 6 событий для одного броска нечетныеэми будут 3.
Следовательно, вероятность нечетного броска равна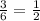
Вероятность того, что произведение чисел бросков будет нечетным равна вероятности двойного нечетного броска - т.е. произведению вероятностей для 1 и 2 броска:
Следовательно, вероятность того, что произведение чисел бросков будет четным равна разности между 1 и Рн:
2. Возможны варианты бросков (первый-второй броски):
1 - чч - четный-четный
2 - чн - четный-нечетный
3 - нч - нечетный-четный
4 - нн - нечетный-нечетный.
Произведение же четно, когда четным является ХОТЯ БЫ ОДИН из множителей.
А это происходит в трех случаях из 4-х - случае 1, 2 и 3 из указанных выше.
То есть
Легко проверить, что вероятность наступления каждого из событий равна:
произведению вероятности четности/нечетности первого броска на вероятность четности/нечетности второго броска.
Для любого броска вероятность четного числа очков равна вероятности нечетного и составляет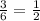
Следовательно:
А значит,
Итак, в двух различных решениях получили одинаковые результаты. Следовательно, ответ верен:
ответ :