Два вектора коллинеарны, если их соответствующие координаты пропорциональны.
Найдём координаты вектора :
Далее найдём координаты вектора :
Разделим соответствующие координаты полученных векторов:
Видим, что координаты пропорциональны (коэффициент пропорциональности равен , то есть имеет место равенство ). Следовательно, векторы коллинеарны.
Два вектора коллинеарны, если их соответствующие координаты пропорциональны.
Найдём координаты вектора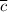 :
:
Далее найдём координаты вектора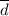 :
:
Разделим соответствующие координаты полученных векторов:
Видим, что координаты пропорциональны (коэффициент пропорциональности равен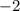 , то есть имеет место равенство
, то есть имеет место равенство 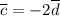 ). Следовательно, векторы коллинеарны.
). Следовательно, векторы коллинеарны.