Для всех остальных x и y: точка не попадает в заштрихованную область.
Пошаговое объяснение:
Левая заштрихованная область — это четверть круга во второй четверти. Круг задаётся неравенством . Ограничения второй четверти: x ≤ 0, y ≥ 0.
Правая заштрихованная область — это область выше некоторого модуля. Модуль задаётся уравнением . Так как модуль опущен на R вниз, то c = -R. Так как "вершина" модуля сдвинута на R/2 вправо, то b = R/2. Известно, что точка (0; 0) принадлежит графику модуля. Найдём a:
Тогда искомое уравнение:
Нужное нам неравенство задаётся так: . Дополнительно также нужно ограничение y ≤ 0.
Для x ≤ 0 и y ≥ 0: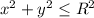
Для x > 0 и y ≤ 0:
Для всех остальных x и y: точка не попадает в заштрихованную область.
Пошаговое объяснение:
Левая заштрихованная область — это четверть круга во второй четверти. Круг задаётся неравенством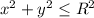 . Ограничения второй четверти: x ≤ 0, y ≥ 0.
. Ограничения второй четверти: x ≤ 0, y ≥ 0.
Правая заштрихованная область — это область выше некоторого модуля. Модуль задаётся уравнением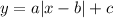 . Так как модуль опущен на R вниз, то c = -R. Так как "вершина" модуля сдвинута на R/2 вправо, то b = R/2. Известно, что точка (0; 0) принадлежит графику модуля. Найдём a:
. Так как модуль опущен на R вниз, то c = -R. Так как "вершина" модуля сдвинута на R/2 вправо, то b = R/2. Известно, что точка (0; 0) принадлежит графику модуля. Найдём a:
Тогда искомое уравнение: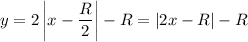
Нужное нам неравенство задаётся так: . Дополнительно также нужно ограничение y ≤ 0.
. Дополнительно также нужно ограничение y ≤ 0.