Уравнение окружности с центром в точке (х,у) и радиусом R запишется следующим образом
Здесь координатными осями и неизвестными будут уже и .
Любимые неизвестные х и у оказались занятыми.:)
Так как радиус окружности известен, то подставим вместо него 6.
Если точка A (a, b) принадлежит кругу, то удовлетворяет уравнению (1), а также попадает внутрь этой окружности, это выразится неравенством
.
Все, чт меньше радиуса окружности, попадет внутрь круга. Знак равенства в неравенстве говорит о принадлежности к границе круга.
Вместо подставим а, вместо - b.
То есть выполняется неравенство
Уравнение окружности с центром в точке (х,у) и радиусом R запишется следующим образом
Здесь координатными осями и неизвестными будут уже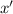 и
и 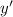 .
.
Любимые неизвестные х и у оказались занятыми.:)
Так как радиус окружности известен, то подставим вместо него 6.
Если точка A (a, b) принадлежит кругу, то удовлетворяет уравнению (1), а также попадает внутрь этой окружности, это выразится неравенством
Все, чт меньше радиуса окружности, попадет внутрь круга. Знак равенства в неравенстве говорит о принадлежности к границе круга.
Вместо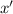 подставим а, вместо
подставим а, вместо 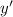 - b.
- b.
То есть выполняется неравенство