Пошаговое объяснение:
ОДЗ:
Таким образом, вашего ответа уже быть не может!
Продолжим решение:
Т.к. , то:
С учетом ОДЗ:
Неравенство решено!
㏒₅((3-х)*(х²+2))≥㏒₅(х²-7х+12)+㏒₅(5-х)
ОДЗ
3-х>0⇒x<3
х²-7х+12>0⇒(x-3)(x-4)>0 /корни левой части по Виета нашел х=3, х=4/
___34
+ - + ⇒ х∈(-∞;3)∪(4;+∞)
5-x>0⇒х∈(-∞;5), окончательно ОДЗ х∈(-∞;3)
Т.к. 5>1, то логарифмическая функция возрастает, и
(3-х)*(х²+2)≥(х-3)(х-4)(5-х)⇒(3-х)*(х²+2)-(х-3)(х-4)(5-х)≥0
(3-х)*(х²+2)+(3-х)(х-4)(5-х)≥0
(3-х)*(х²+2+(х-4)(5-х))≥0; (3-х)*(х²+2+9х-х²-20)≥0;
(3-х)*(9х-18)≥0; решим неравенство методом интервалов.
х=3; х=2.
23___
- + -
х∈[2;3) с учетом одз, получим ответ х∈[2;3)
Пошаговое объяснение:
ОДЗ:
Таким образом, вашего ответа уже быть не может!
Продолжим решение:
Т.к.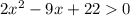 , то:
, то:
С учетом ОДЗ:
Неравенство решено!
㏒₅((3-х)*(х²+2))≥㏒₅(х²-7х+12)+㏒₅(5-х)
ОДЗ
3-х>0⇒x<3
х²-7х+12>0⇒(x-3)(x-4)>0 /корни левой части по Виета нашел х=3, х=4/
___34
+ - + ⇒ х∈(-∞;3)∪(4;+∞)
5-x>0⇒х∈(-∞;5), окончательно ОДЗ х∈(-∞;3)
Т.к. 5>1, то логарифмическая функция возрастает, и
(3-х)*(х²+2)≥(х-3)(х-4)(5-х)⇒(3-х)*(х²+2)-(х-3)(х-4)(5-х)≥0
(3-х)*(х²+2)+(3-х)(х-4)(5-х)≥0
(3-х)*(х²+2+(х-4)(5-х))≥0; (3-х)*(х²+2+9х-х²-20)≥0;
(3-х)*(9х-18)≥0; решим неравенство методом интервалов.
х=3; х=2.
23___
- + -
х∈[2;3) с учетом одз, получим ответ х∈[2;3)