Предположим, что х – это весь путь пройденный ледоколом, тогда в первый день он проплыл 0,4x, следовательно, во второй день 0,625(x-0,4x) или 0,375х, а в третий день - оставшиеся 90 км
согласно этим данным составим и решим уравнение:
0,4х+0,375х+90=х
0,775х+90=х
х-0,775х=90
0,225х=90
х=90:0,225
х=400 (км) - весь путь.
0,4х=0,4·400=160 (км) - проплыл ледокол в первый день.
0,375х=0,375·400=150 (км) - проплыл ледокол во второй день.
ответ: в первый день ледокол проплыл 160 км, а во второй - 150 км.
Предположим, что х – это весь путь пройденный ледоколом, тогда в первый день он проплыл 0,4x, следовательно, во второй день 0,625(x-0,4x) или 0,375х, а в третий день - оставшиеся 90 км
согласно этим данным составим и решим уравнение:
0,4х+0,375х+90=х
0,775х+90=х
х-0,775х=90
0,225х=90
х=90:0,225
х=400 (км) - весь путь.
0,4х=0,4·400=160 (км) - проплыл ледокол в первый день.
0,375х=0,375·400=150 (км) - проплыл ледокол во второй день.
ответ: в первый день ледокол проплыл 160 км, а во второй - 150 км.
Для ремонта двух книг Косте нужно три часа,сколько нужно времени для ремонта а) 4 книг, б) 6 книг, в) 8 книг
2 к. - 3 ч
1 к. - ? ч
а) 4 к. - ? ч
б) 6 к. - ? ч
в) 8 к. - ? ч час=60 мин ⇒ 3 часа=180 мин
180:2=90 (мин) - потребуется на ремонт одной книги.
а) 4·90=360 (мин) или 6 (ч) - потребуется на ремонт 4 книг.
б) 6·90=540 (мин) или 9 (ч) - потребуется на ремонт 6 книг.
в) 8·90=720 (мин) или 12 (ч) - потребуется на ремонт 8 книг ч) - время на ремонт 1 книги.
а)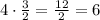
(ч) - потребуется на ремонт 4 книг.
б)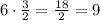
(ч) - потребуется на ремонт 6 книг.
в)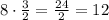
(ч) - потребуется на ремонт 8 книг.
ответ: 6 часов; 9 часов и 12 часов.