Заметим, что при нахождении обратных чисел для чисел из этого промежутка, мы будем однозначно получать числа из промежутка .
Рассмотрим промежуток .
Заметим, что если мы будем находить числа, на 1 меньшие, чем числа из данного промежутка, мы будем однозначно получать числа из промежутка .
Таким образом, по некоторому числу из промежутка однозначно определяется число из промежутка .
Получим отображение:
Рассуждая в обратном направлении можно получить обратное отображение. Прибавляя 1 к некоторому числу из промежутка , а затем находя для получившегося числа обратное, мы будем однозначно получать числа из промежутка .
Но по условию вместо промежутка рассматривается промежуток , а вместо промежутка - промежуток . Тогда, сопоставим нули в этих промежутках друг другу.
Рассмотрим промежуток
.
Заметим, что при нахождении обратных чисел для чисел из этого промежутка, мы будем однозначно получать числа из промежутка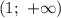
.
Рассмотрим промежуток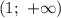
.
Заметим, что если мы будем находить числа, на 1 меньшие, чем числа из данного промежутка, мы будем однозначно получать числа из промежутка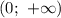
.
Таким образом, по некоторому числу из промежутка
однозначно определяется число из промежутка 
.
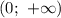Получим отображение:
Рассуждая в обратном направлении можно получить обратное отображение. Прибавляя 1 к некоторому числу из промежутка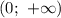
, а затем находя для получившегося числа обратное, мы будем однозначно получать числа из промежутка 
.
Но по условию вместо промежутка
рассматривается промежуток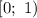 
, а вместо промежутка 
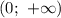- промежуток 
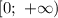. Тогда, сопоставим нули в этих промежутках друг другу.
Получим прямое отображение:
Получим обратное отображение:
Пошаговое объяснение:
аₙ=а₁+(n-1)d
а₁ - первый член последовательности
аₙ - член занимающий место n ( 1,2,...n.)
n - номер члена
d - разность между членами ("добавка" которую прибавляют к каждому,чтобы получить последующий)
а₁=2 d=3 2, 2+3, 2+3*2,2+3*3,2+3*4 2 , 5 , 8 , 11 , 14
а₁=0,2 d=0,3 0,2 ; 0,2+0,3 ; 0,2+0,3*2 ; 0,2+0,3*3 ; 0,2+0,3*4
0,2 ; 0,5 ; 0,8 ; 1,1 ; 1,4
а₁= - 0,2 d=0,3 - 0,2 ; -0,2+0,3 ; -0,2+0,3*2 ; -0,2+0,3*3 ; -0,2+0,3*4
- 0,2 ; 0,1 ; 0,4 ; 0,7 ; 1
а₁= 1/2=3/6, d=1/3=2/6 (так легче считать)
3/6 ; 3/6+2/6=5/6 ; 3/6+2/6*2=7/6 ;3/6+2/6 *3=9/6 ;3/6+2/6 *4=11/6
1/2 ; 5/6 ; 1 1/6 ; 1 1/2 ;1 5/6;
а₁= -1/2=3/6, d=-1/3=-2/6 (так легче считать)
-3/6; -3/6-2/6=-5/6; -3/6-2/6*2=-7/6=-1 1/6;-3/6-2/6 *3=-9/6=-1 1/2;
-3/6-2/6 *4=-11/6=-1 5/6
-1/2 ; -5/6 ; -1 1/6 ;- 1 1/2 ; -1 5/6;
а₁= -1/2=3/6, d=1/3=2/6 (так легче считать)
-3/6 ; -3/6+2/6=-1/6 ; -3/6+2/6*2=1/6 ;-3/6+2/6 *3=3/6 ;-3/6+2/6 *4=5/6
-1/2 ; -1/6 ; 1/6 ; 1/2 ; 5/6;