А теперь смотрим, если первым вытянули белый шар, то в коробке осталось 6 белых шаров из 9 оставшихся, тогда второй белый шар будет вынут с вероятностью 6/9=2/3.
Если первым вытянули черный шар, то в коробке осталось 7 белых шаров из 9 оставшихся, тогда второй белый шар будет вынут с вероятностью 7/9
Задача на полную вероятность:
Гипотезы:
B - первым вынули белый шар.
C - первым вынули черный шар.
P(B)=7/10
P(C)=3/10
A-вторым вынули белый шар.
Условные вероятности:
A/B - вторым вынули белый шар, при условии что первым вынули белый шар.
A/C-вторым вынули белый шар, при условии что первым вынули черный шар.
√26sin(α+π/2), если ctgα=-5 , 0°<α<180°. Не могу понять как выбрать знак при косинусе ведь он лежит между 180 и 0
Пошаговое объяснение:
{ctgα=-5 ( котангенс отрицателен во 2и 4 четвертях)
{ 0°<α<180° ( это 1 и 2 четверти)
Из этих двух условий следует , что α∈ II четверти. Во 2 четверти cosα<0.
√26sin(α+π/2)= √26cosα
Т.к 1+ctg²α=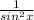
, то 1+(-5)²=
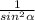, sin²α=1/26.
По основному тригонометрическому тождеству
sin²α+cos²α=1
1/26+cos²α=1
cos²α=1-1/26
cos²α=25/26
cosα= -√(25/26) , cosα= -5/√26.
√26sin(α+π/2)= √26cosα= √26*(-5/√26)= -5
0.7
Пошаговое объяснение:
всего в коробке 7+3=10 шаров
вероятность вынуть первый белый шар равна 7/10
вероятность вынуть первый черный шар равна 3/10
А теперь смотрим, если первым вытянули белый шар, то в коробке осталось 6 белых шаров из 9 оставшихся, тогда второй белый шар будет вынут с вероятностью 6/9=2/3.
Если первым вытянули черный шар, то в коробке осталось 7 белых шаров из 9 оставшихся, тогда второй белый шар будет вынут с вероятностью 7/9
Задача на полную вероятность:
Гипотезы:
B - первым вынули белый шар.
C - первым вынули черный шар.
P(B)=7/10
P(C)=3/10
A-вторым вынули белый шар.
Условные вероятности:
A/B - вторым вынули белый шар, при условии что первым вынули белый шар.
A/C-вторым вынули белый шар, при условии что первым вынули черный шар.
P(A/B)=2/3
P(A/C)=7/9
Формула полной вероятности:
P(A)=P(B)*P(A/B)+P(C)*P(A/C)