Какие существуют подходы к обоснованию типов коммуникации? в чем состоит отличие устно-речевой и письменно-речевой коммуникации?

Задача. Фирма среди своих сотрудников разыгрывает новогоднюю лотерею. В лотерее 10 билетов, из которых 6 выигрышных. Сотрудник фирмы покупает 2 билета. Какова вероятность того, что у этого сотрудника выиграет хотя бы один билет? Результат округлите до сотых.

Количество возможных элементарных исходов равно числу вынуть два билета из 10 билетов, т.е. .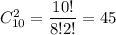

Подсчитаем количество благоприятных исходов. Для этого нужно определить сколькими этот сотрудник может выбрать хотя бы один выигрышный билет. Таких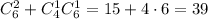

Искомая вероятность: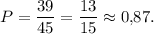

* * * * * * * * * * * * * * * * * * * * * * * * * * *

13. а) Решите уравнение 2cos(2x - π/3) - sinx =√3sin2x.

б) Найдите все корни данного уравнения принадлежащие отрезку [-5π ; 3π/2].

ответ:  13. а) - π/2 +2πn ; π/6 +2πn  или  5π/6 +2πk, где  n , k ∈  ℤ .

13. б) { - 4,5π ;-23π/6 ; -2,5π ; - 11π/6 ; -0,5π ;  π/6 ; 1, 5π  ;  13π/6} .

Пошаговое объяснение:  

13. a)

2cos(2x - π/3) - sinx =√3sin2x ⇔

2( cos2x*cos(π/3) +sin2x*sin(π/3) ) - sinx = √3sin2x ⇔

2( cos2x*(1/2) +sin2x*(√3 /2) ) - sinx = √3sin2x ⇔

cos2x +√3sin2x - sinx  = √3sin2x  ⇔

cos2x - sinx  = 0 ⇔ 1 -2sin²x -sinx =0 ⇔ 2sin²x+sinx - 1 = 0 ⇒

квадратное уравнение относительно   sinx  

sinx₁, ₂  =  (-1 ±3) / 4  ⇒ sinx₁ = - 1 ;  sinx₂  = 1/2.

но и так было очевидно: sinx = -1  ⇒ и  еще по т Виета  sinx = 1/2

* * *  sin²x + (1/2)sinx + 1/2=0 ⇔ sin²x - (-1+1/2)sinx + (-1)*1/2=0  Виет * * *

!     sinx = a , |a| ≤ 1  ⇒  x = (-1)ⁿ arcsin(a) +πn , n ∈  ℤ

1 )   sinx₁= - 1     x = (-1)ⁿ (- π/2) +πn , n ∈  ℤ

иначе:   x₁ = - π/2 +2πn , n ∈  ℤ  ;

2 )  sinx₂  = 1/2.       x₂ = (-1)ⁿ(π/6) +πn , n ∈  ℤ

иначе: x₂ =π/6 +2πn  или  x₂ =5π/6 +2πk, где  n , k ∈  ℤ .

13. б)   ! Намного лучше с тригонометрической окружности  или методом полного перебора

* * *   sinx = - 1   ⇒ x = - π/2 +2πn , n ∈  ℤ .                                  * * *

* * *   sinx = 1 /2  ⇒ x =π/6 +2πn  или  x =5π/6 +2πk ; n , k ∈  ℤ  * * *

б₁ )

- 5π ≤ - π/2 +2πn  ≤  3π/2 ⇔  - 5π + π/2≤ 2πn  ≤  3π/2+ π/2 ⇔    

- 9π/2 ≤ 2πn ≤ 2π ⇔ - 9/4 ≤ n ≤  1 ⇒ n  =  -2 ; -1; 0 ; 1 .

- 4,5π ; -2,5π ;  -0,5π ;  1, 5π .

- - - - - - -

б ₂)

- 5π ≤ π/6 +2πn ≤ 7π/2 ⇔ - 5π - π/6 ≤ 2πn  ≤7π/2- π/6 ⇔

- 31π/6 ≤ 2πn  ≤ 10/3  ⇔ - 31/12 ≤ n  ≤ 5/3  

n  ∈ { -2 ; -1 ; 0;  1 }  

x ∈{ -23π/6 ; - 11π/6 ;  π/6 ; 13π/6 }   ариф. прогрессия d =2π

б ₃)

- 5π ≤ 5π/6 +2πk ≤ 7π/2  ||*6|| ⇔ -30π ≤ 5π +12πk ≤ 21π  || : π >0||⇔

-30 ≤ 5 +12k ≤ 21 ⇔-35 ≤ 12k ≤  16 ⇔  -35 /12 ≤ k ≤ 4/3

k ∈ { -2 ; -1 ; 0;  1 }  

x ∈{ -23π/6 ; - 11π/6 ;  π/6 ; 13π/6 }   ариф. прогрессия d =2π

* * * * * * * * * * * * * * * * * * * * * * * * * * *

2sin²x+sinx - 1 = sin²x +sinx +sin²x -1 =sinx(sinx+1) +(sinx+1)(sinx -1) =

(sinx+1)(sinx+sinx -1) = (sinx+1)(2sinx -1) =2(sinx+1)(sinx-1/2)      a(t -t₁)(t -t₂)