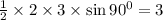Пусть угол между сторонами a и b равен φ. Тогда площадь треугольника равна ; Пусть произведение ab максимально, то есть равно 6. Сторона c не участвует в формировании величины площади. Однако от c зависит максимальность синуса. По теореме косинусов: ; Подставив максимальные значения a и b, а также минимальное значение косинуса ⇔ максимальное значение синуса, придем к тому, что , при этом значение c лежит в диапазоне. Итак, максимальная площадь треугольника равна
Пусть угол между сторонами a и b равен φ. Тогда площадь треугольника равна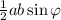 ; Пусть произведение ab максимально, то есть равно 6. Сторона c не участвует в формировании величины площади. Однако от c зависит максимальность синуса. По теореме косинусов:
; Пусть произведение ab максимально, то есть равно 6. Сторона c не участвует в формировании величины площади. Однако от c зависит максимальность синуса. По теореме косинусов: 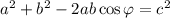 ; Подставив максимальные значения a и b, а также минимальное значение косинуса ⇔ максимальное значение синуса, придем к тому, что
; Подставив максимальные значения a и b, а также минимальное значение косинуса ⇔ максимальное значение синуса, придем к тому, что 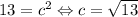 , при этом значение c лежит в диапазоне. Итак, максимальная площадь треугольника равна
, при этом значение c лежит в диапазоне. Итак, максимальная площадь треугольника равна