ответ:
пошаговое объяснение:
полное решение составляется из 2:
1) общее решение однородного уравнения т.е. уравнения y"+9y=0
2) и частного решеня неоднородного (т.е. того что вы написали)
для нахождения общее решение однородного уравнения запишем характеристическое уравнение
k^2+9=0 => k=3 и k=-3
тогда общее решение однородного уравнения запишется так a*e(3x)+b*e(-3x)
частного решеня неоднородного будем искать в виде(в виде правой части нашего уравнения)
y= c*e(3x)
найдем y"
y'= c*3*e(3x) y"= c*9*e(3x)
подставим в уравнение получим
c*9*e(3x) + 9*c*e(3x) = 6*e(3x) ==> c*9 + 9*c = 6 ==> 18*c=6 ==> c=6/18=1/3
полное решение будет
y = a*e(3x)+b*e(-3x) +1/3*e(3x) =(a+1/3)*e(3x)+b*e(-3x)
подробнее - на -
Для начала нужно решить соответствующее линейное однородное дифференциальное уравнение, выполнив замену .
Общее решение однородного диф. уравнения: .
Рассмотрим функцию . Здесь , где , Сравнивая с корнями характеристического уравнения и принимая во внимая, что
Определим первые две производные функции частного решения и подставляем в исходное дифференциальное уравнение одновременно разделив обе части на .
Приравниваем коэффициенты при степенях x
Общее решение линейного неоднородного дифференциального уравнения ищем как сумму общего однородного диф. уравнения и частного решения
ответ:
пошаговое объяснение:
полное решение составляется из 2:
1) общее решение однородного уравнения т.е. уравнения y"+9y=0
2) и частного решеня неоднородного (т.е. того что вы написали)
для нахождения общее решение
однородного уравнения запишем характеристическое уравнение
k^2+9=0 => k=3 и k=-3
тогда общее решение однородного уравнения запишется так a*e(3x)+b*e(-3x)
частного решеня неоднородного будем
искать в виде(в виде правой части нашего уравнения)
y= c*e(3x)
найдем y"
y'= c*3*e(3x) y"= c*9*e(3x)
подставим в уравнение получим
c*9*e(3x) + 9*c*e(3x) = 6*e(3x) ==> c*9 + 9*c = 6 ==> 18*c=6 ==> c=6/18=1/3
полное решение будет
y = a*e(3x)+b*e(-3x) +1/3*e(3x)
=(a+1/3)*e(3x)+b*e(-3x)
подробнее - на -
Для начала нужно решить соответствующее линейное однородное дифференциальное уравнение, выполнив замену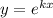 .
.
Общее решение однородного диф. уравнения: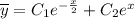 .
.
Рассмотрим функцию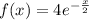 . Здесь
. Здесь 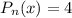 , где
, где 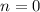 ,
, 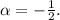 Сравнивая
Сравнивая 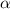 с корнями характеристического уравнения и принимая во внимая, что
с корнями характеристического уравнения и принимая во внимая, что
Определим первые две производные функции частного решения и подставляем в исходное дифференциальное уравнение одновременно разделив обе части на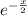 .
.
Приравниваем коэффициенты при степенях x
Общее решение линейного неоднородного дифференциального уравнения ищем как сумму общего однородного диф. уравнения и частного решения