Катер шел 3 ч против течения реки и 2ч по течению. какой путь катер за эти 5ч, если собственная скорость катера 18,6 км. ч., а скорость течения реки 1,3 км. ч.
Заметим, что если x является решением уравнения, то и -x также является решением уравнения (действительно, возведение в квадрат, в четвёртую степень и взятие косинуса "убивает" минус). Значит, необходимое условие единственности решения: x = -x ⇒ x = 0 (условие не достаточное, так как помимо 0 могут быть и другие решения, поэтому каждое значение параметра необходимо будет проверить).
Подставим x = 0 в уравнение:
Если a = 0, то уравнение имеет вид:
Три решения, a = 0 не подходит.
Если a = -1:
Заметим, что , а , то есть левая часть не меньше нуля, а правая — не больше нуля. Равенство достигается, когда обе части равны нулю:
-1
Пошаговое объяснение:
Заметим, что если x является решением уравнения, то и -x также является решением уравнения (действительно, возведение в квадрат, в четвёртую степень и взятие косинуса "убивает" минус). Значит, необходимое условие единственности решения: x = -x ⇒ x = 0 (условие не достаточное, так как помимо 0 могут быть и другие решения, поэтому каждое значение параметра необходимо будет проверить).
Подставим x = 0 в уравнение:
Если a = 0, то уравнение имеет вид:
Три решения, a = 0 не подходит.
Если a = -1:
Заметим, что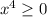
, а 
, то есть левая часть не меньше нуля, а правая — не больше нуля. Равенство достигается, когда обе части равны нулю:
При каких значениях параметра a уравнение
(5ˣ)² - (8a+5)*5ˣ +16a² +20a -14 =0 имеет единственное решение
Решение : (5ˣ)² - (8a+5)*5ˣ +16a² +20a -14 =0
квадратное уравнение относительно t = 5ˣ >0
t² - (8a+5)t +16a² +20a +14 =0
D = (8a+5)² - 4(16a² +20a -14 )=64a² +80a +25 -64a² -80a+56 =81 =9² >0
т.е. это уравнение всегда имеет 2 решения
Но если свободный член будет отрицательно , то корни будут разных знаков и исходное уравнение будет иметь одно решение
16a² +20a - 14 =16(a +7/4)(a - 1/2) < 0 ⇒ a ∈( -7/4 ; 1/2 )
НО ЕСЛИ 16a² +20a - 14 =0 , т.е. a = -7/4 или a = 1/2
получается
5ˣ (5ˣ - 8a - 5) = 0 ⇒ 5ˣ = 0 или 5ˣ = 8a + 5
5ˣ = 0 не имеет решение 5ˣ = 8a + 5 имеет решение если
a > - 5 / 8 || a = 1/2 удовлетворяет ||
следовательно
ответ: a ∈( -7/4 ; 1/2 ]
5ˣ = (8a+5 -9)/2 = 4a -2
5ˣ = (8a+5 +9)/2 = 4a +7