Каждое число в ряду 4,23,12 увеличить на 2 десятка.Найди сумму всех полученных чисел.
​

ответ:
скорость первого = 5 км/ч
скорость второго = 5,8 км/ч

Решение:
Пусть х - скорость первого, у - скорость второго. Зная, что каждый из них был в пути 5 часов и то, что разность их расстояний равна 4, составляем уравнение:
5у - 5х = 4
5у = 4 +5х
у = (4+5х) : 5

Зная, что сумма расстояний равна 54, составляем второе уравнение и подставляем в него значение у.
5х + 5у = 54
5х + 5 * ((4 + 5х) : 5) = 54
5х + 4 + 5х = 54
10 х = 50
х = 5 (км/ч) - скорость первого туриста

(4 + 5*5) : 5 = 29 : 5 = 5, 8 (км/ч) - скорость второго туриста.

Решаем данное уравнение как квадратное уравнение относительно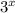

Если D = 0, т.е. a+1 = 0 откуда  a = -1, то подставляя этот параметр в исходное уравнение, мы получим

Это уравнение решений не имеет, т.к. левая часть уравнения принимает только положительные значения.

Если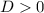 , т.е. a + 1 > 0   откуда   a>-1, то нам нужны лишь те корни, которые приобретают разные знаки, т.е. по теореме Виета:

Подставим параметры a = 1 и a = 7 в исходное уравнение, получим

a=1 :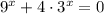

Это уравнение корней не имеет, т.к. левая часть уравнения всегда положительно.

a = 7: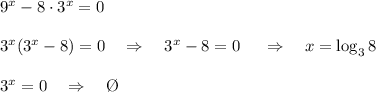

Т.е. исходное уравнение имеет единственный корень только при