Каждую клетку квадратной таблицы 3×3 можно раскрасить черным, красным, синим или зеленым цветом. Сколько существует различных вариантов закрашивания фигуры?
• Обыск осуществляется следователем ,который принимает решение о выполнении какого-либо действия. Следователь должен все расчитать , вплоть до мелочей.
• Чтобы произвести обыск следователь должен: собрать всю, необходимую следствию , информацию, спланировать действий при обыске, распределить обязаннасти каждого участника обыска. рассмотреть все возможные варианты поведения обыскиваемого, наличие огнестрельного оружия, использование специального оборудования ...
• Р.С. Белкин выделяет три основные категории сбора информации: о личности обыскиваемого и всех окружающих его лицах, об искомых объектах и о месте обыска.
- Сбор информации о личности обыскиваемого. От следователя требуется узнать: ФИО, год рождения, семейное положение, образование, профессия, место работы, судимость и состояние здоровья, умственные качества подозреваемого...
В случяе отказа в обыске со стороны обыскиваемого, следователь будет строить тактику принудительного обыска.
- Сбор информации о искомых объектах: включает в себя детальное изучение месности , всех запасных выходов, и других подобных объектах. Производится с целью разузнать наиболее вероятные места, в которых можно спрятать искомый объект.
Сбор такой информации следователь может найти через следующии источники: доприс сведетелей , снятие следов с места происшествия , показания самого потерпевшего и др.
- Сбор информации о месте обыска:нужно собрать сведения не только об месте проживания обыскиваемого ,но и об других возможных помещениях, которые могут послужить как укрытием от следствия.
• А также у следователя должны присутствовать все необходимые, в данном случае, инструменты для проведения обыска.
До точки экстремума функция возрастает, а после — убывает. Значит, это точка максимума. Максимальное значение функции равно . Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
ответ:
8. При изменении размеров пирамиды соотношения между соответственными элементами не изменятся, поэтому примем для простоты вычислений сторону основания за 1.
Рассмотрим первую пирамиду:
Пусть SKM — сечение пирамиды SABCD, где K и M — середины BC и AD соответственно. Тогда в это сечение попадает окружность, вписанная в треугольник SKM и касающаяся KM в точке S' (проекция точки S), SK в точке K'. Пусть ∠SKS' = α, KO₁ — биссектриса, тогда:
Учитывая, что угол находится в первой четверти,
Рассмотрим вторую пирамиду:
Пусть S₁A₁C₁ — сечение пирамиды S₁A₁B₁C₁D₁. Это сечение содержит окружность, вписанную в треугольник S₁A₁C₁, касающуюся стороны A₁C₁ в точке S₁' (проекция точки S₁) и стороны S₁A₁ в точке A₁'. Пусть ∠S₁A₁S₁' = β, A₁O₂ — биссектриса. Тогда:
• Обыск осуществляется следователем ,который принимает решение о выполнении какого-либо действия. Следователь должен все расчитать , вплоть до мелочей.
• Чтобы произвести обыск следователь должен: собрать всю, необходимую следствию , информацию, спланировать действий при обыске, распределить обязаннасти каждого участника обыска. рассмотреть все возможные варианты поведения обыскиваемого, наличие огнестрельного оружия, использование специального оборудования ...
• Р.С. Белкин выделяет три основные категории сбора информации: о личности обыскиваемого и всех окружающих его лицах, об искомых объектах и о месте обыска.
- Сбор информации о личности обыскиваемого. От следователя требуется узнать: ФИО, год рождения, семейное положение, образование, профессия, место работы, судимость и состояние здоровья, умственные качества подозреваемого...
В случяе отказа в обыске со стороны обыскиваемого, следователь будет строить тактику принудительного обыска.
- Сбор информации о искомых объектах: включает в себя детальное изучение месности , всех запасных выходов, и других подобных объектах. Производится с целью разузнать наиболее вероятные места, в которых можно спрятать искомый объект.
Сбор такой информации следователь может найти через следующии источники: доприс сведетелей , снятие следов с места происшествия , показания самого потерпевшего и др.
- Сбор информации о месте обыска:нужно собрать сведения не только об месте проживания обыскиваемого ,но и об других возможных помещениях, которые могут послужить как укрытием от следствия.
• А также у следователя должны присутствовать все необходимые, в данном случае, инструменты для проведения обыска.
7.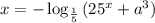
Пусть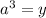 , количество корней от этого не изменится.
, количество корней от этого не изменится.
Рассмотрим функцию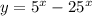 :
:
До точки экстремума функция возрастает, а после — убывает. Значит, это точка максимума. Максимальное значение функции равно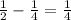 . Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
. Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
ответ:![(0; \frac{\sqrt[3]{2}}{2})](/tpl/images/0445/7312/80965.png)
8. При изменении размеров пирамиды соотношения между соответственными элементами не изменятся, поэтому примем для простоты вычислений сторону основания за 1.
Рассмотрим первую пирамиду:
Пусть SKM — сечение пирамиды SABCD, где K и M — середины BC и AD соответственно. Тогда в это сечение попадает окружность, вписанная в треугольник SKM и касающаяся KM в точке S' (проекция точки S), SK в точке K'. Пусть ∠SKS' = α, KO₁ — биссектриса, тогда:
Учитывая, что угол находится в первой четверти,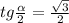
Рассмотрим вторую пирамиду:
Пусть S₁A₁C₁ — сечение пирамиды S₁A₁B₁C₁D₁. Это сечение содержит окружность, вписанную в треугольник S₁A₁C₁, касающуюся стороны A₁C₁ в точке S₁' (проекция точки S₁) и стороны S₁A₁ в точке A₁'. Пусть ∠S₁A₁S₁' = β, A₁O₂ — биссектриса. Тогда:
Решая аналогичное уравнение, получаем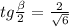
ответ: 4 : 3