Чтобы найти промежутки возрастание/спадания функции и её экстремумы, нужно приравнять её производную к нулю:
Найдём производную про правилу: :
Приравняем производную к нулю:
Знаменатель не может быть равен нулю, значит приравняем к нему только числитель:
Получили экстремумы функции.
Воспользуемся методом интервалов для нахождения промежутков возрастания и спадания функции. Т.к. возле старшего коэффициента стоит плюс, начинаем с плюса:
Чтобы найти промежутки возрастание/спадания функции и её экстремумы, нужно приравнять её производную к нулю:
Найдём производную про правилу: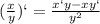 :
:
Приравняем производную к нулю:
Знаменатель не может быть равен нулю, значит приравняем к нему только числитель:
Получили экстремумы функции.
Воспользуемся методом интервалов для нахождения промежутков возрастания и спадания функции. Т.к. возле старшего коэффициента стоит плюс, начинаем с плюса:
+ - +
-------(-3)----------(1)----------->
Функция возрастает на (-∞; -3] и [1; +∞)
Функция спадает на [-3; 1]
x = -3 - точка максимума
x = 1 - точка минимума
ответ: 1 тетрадб=10 тг, 1 альбом = 8тг
20 тетрадей +5 альбомов = 340тг
Известно, что 4а (альбома) дешевле 10т (тетрадей) на 40 тг.
Тогда я из имеющихся 4 альбомов сделаю тетради, получилось
30 тетрадей + 1 альбом.
Если мы прибавили 10 тетрадей, то к общей сумме нужно прибавить 40 тг.
Сумма равна 380 тг.
380тг÷30= 10(ост 80)
В примере выше мы получаем стоимость одной тетради (без остатка). Далее
(80÷10)+10=18 стоимость альбома
Можно проверку сделать. (10×20)+(18×5)= 200+140=340.
Пошаговое объяснение: