Математика: Кесте бойынша есеп құрастыр және шығар

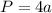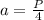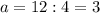
12.Дано:квадрат;P=12см;Найти: d1) = = см - сторона2) По т. Пифагора cмответ: 3√2 см13.Дано:прямоугольник; см cмНайти: d По т. Пифагора смответ: 20 см14.Дано:n-угольник; °Найти: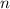 ответ: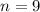 16.Дано:12-угольник;Найти: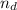 ответ: 5417.Дано: ромб; см смНайти: S Площадь ромба равна половине произведения его диагоналей. см²18/Дано:параллелограмм;∠1+∠2+∠3=220°Найти: меньший уголРешение1) ∠1+∠2+∠3+∠4=360°∠4=360°-220°=140° - это смежный с меньшим2) 180°-140°=40° - меньшийответ: 40°19) Всего (n+3)...

Кесте бойынша есеп құрастыр және шығар

Показать ответ

Ответ:

kekys326

14.04.2022 02:45

Нужно найти такие два натуральных (целых) числа, отношение которых равно отношению двух дробных чисел в задании.

Первый решения:
Отношение- это по сути деление одного числа на другое. Выполним это деление, сократив получившуюся дробь:
$\frac{17}{18}:\frac{7}{12}=\frac{17}{18}*\frac{12}{7}=\frac{17*12}{18*7}=\frac{17*2}{3*7}=\frac{34}{21}=34:21$

Конечно, можно подобрать сколько угодно много пар целых чисел, имеющих то же отношение, что и исходные дроби. Но, существует только одна минимальная пара таких чисел, и мы её получили сокращая дробь (теперь в числителе и знаменателе- взаимно простые числа).

Второй решения (для тех, кто любит повозиться):
Умножим обе дроби на наименьшее общее кратное (НОК) их знаменателей. При этом отношение не изменится, зато вместо дробей мы получим целые числа.

Разложим на простые множители оба знаменателя:
18 = 2 * 9 = 2 * 3 * 3
12 = 2 * 6 = 2 * 2 * 3
Берём каждый простой множитель в максимальном количестве, которое встретилось в разложении одного из знаменателей.
НОК (18,12) = 2 * 2 * 3 * 3 = 36
Теперь умножаем на 36 обе дроби в отношении, сокращаем дроби, и получаем отношение целых чисел:
$\frac{17}{18}:\frac{7}{12}=\frac{17*36}{18}:\frac{7*36}{12}=\frac{17*2}{1}:\frac{7*3}{1}=34:21$