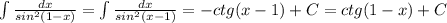Следует применять подстановку так, что бы полностью избавиться от знака радикала. Поскольку в знаменателе присутствует 3 и 4 степень то применяем подстановку 2) = 2x - 1; x = (t¹² +1)/2; dx = 6t¹¹
Теперь нужно сделать обратную подстановку
11. Укажите соответствие между функциями и их неопределенными интегралами
общая сумма углов образованных секущей с двумя параллельными прямыми равна 720
у нас 6 углов = 636
не хватает 2-х углов - их сумма 720-636 =84
сумма смежных углов 180 - не годится
сумма односторонних 180 - не годится
остаются соответственные, вертикальные, накрестлежащие
84/2 = 42
тогда смежный угол 180-42=138
4 е угла полюбому дают сумму 360
138*2<два угла по 138
42*2 <два угла по 42
остается неизвестная сумма 636-360=276
276/2 =138 <два угла по 138
ОТВЕТ 4 угла по-138 2 угла по-42
ответ: t¹² = 2x - 1
11. 1)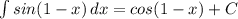
2)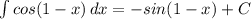
3)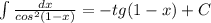
4)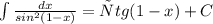
Пошаговое объяснение:
10. В неопределенном интеграле![\int\limits{\frac{\sqrt{2x-1} }{\sqrt[3]{2x-1} +\sqrt[4]{2x-1} } } \, dx](/tpl/images/0132/5542/a0680.png) следует применить подстановку
следует применить подстановку
1) t⁴ = 2x - 1; 2) t¹² = 2x - 1; 3) t³ = 2x - 1; 4) t² = 2x - 1;
Следует применять подстановку так, что бы полностью избавиться от знака радикала. Поскольку в знаменателе присутствует 3 и 4 степень то применяем подстановку 2) = 2x - 1; x = (t¹² +1)/2; dx = 6t¹¹
Теперь нужно сделать обратную подстановку![t=\sqrt[12]{2x-1}](/tpl/images/0132/5542/36e63.png)
11. Укажите соответствие между функциями и их неопределенными интегралами
1.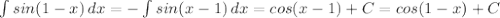
Проверка:(cos(1-x))' = -sin(1 - x)*(1 - x)' = sin(1 - x)
2.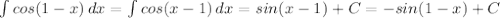
3.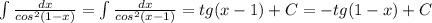
4.