Можно, конечно, начертить графики и увидеть, что пересечений нет, но я напишу более строгое доказательство.
Чтобы уравнение имело решения, нужно чтобы область значений функции включала в себя ноль.
Найдем область значений функции . Для этого найдем точки экстремума.
Так как при x < 0 y' < 0, а при x > 0 y' > 0, то x = 0 - точка минимума, в ней достигается наименьшее значение функции. Найдем его: для этого ноль необходимо подставить в исходную функцию.
y(0) = e⁰ - 0 = 1 - 0 = 1 > 0.
Уже сразу видно, что уравнение не имеет решений, т.к. если минимум функции больше 0, то понятно, что и любое другое значение функции тоже больше 0, а значит значение функции никогда не может равняться нулю и равенство выполняться не может, т.е. уравнения не имеет решений.
S V t
| ? 35 км / ч . 4 ч.
|| ? 31 км / ч . 2 ч .
1) . S^1 = V * t .
S^1 = 35 * 4 = 140 ( км ) .
2) . S^2 = V * t .
S^2 = 31 * 2 = 62 ( км ) .
3) . Cр = 140 + 62 =202 .
Ср = 202 : 2 = 101 ( км/ч ) .
ответ : Ср = 101 км/ ч .
Надеюсь правильно :
Всем удачи , счастья и добра :
Если не сложно поставьте идеальный ответ или лучший
Заранее ОГРОМНОЕ
Если есть вопросы пишите всем отвечу :
Можно, конечно, начертить графики и увидеть, что пересечений нет, но я напишу более строгое доказательство.
Чтобы уравнение имело решения, нужно чтобы область значений функции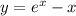
включала в себя ноль.
Найдем область значений функции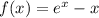
. Для этого найдем точки экстремума.
Так как при x < 0 y' < 0, а при x > 0 y' > 0, то x = 0 - точка минимума, в ней достигается наименьшее значение функции. Найдем его: для этого ноль необходимо подставить в исходную функцию.
y(0) = e⁰ - 0 = 1 - 0 = 1 > 0.
Уже сразу видно, что уравнение не имеет решений, т.к. если минимум функции больше 0, то понятно, что и любое другое значение функции тоже больше 0, а значит значение функции никогда не может равняться нулю и равенство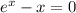
выполняться не может, т.е. уравнения 
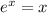не имеет решений.
ОТВЕТ: 0.