Поскольку графиком производной y' = 3x² - 6x - 9 является парабола веточками вверх, то отрицательные значения производной будут находиться между корнями х₁ и х₂.
Поэтому в точке х₁ производная меняет знак с + на -. И это точка максимума.
В точке х₂ производная меняет знак с - на +, значит, это точка минимума.
ответ: в точке x₁ = 0,5(1 - √13) имеет место локальный максимум,
в точке x₂ = 0,5(1 + √13) имеет место локальный минимум
1) Определим значения выражения при различных значениях как последовательность
2) Определим значения членов последовательности при n=1, n=2, n = 3:
3) Применим метод математической индукции.
3a) Возьмем такой член , который кратен 9 (как мы убедились выше, такое существует (например, а3))
Т.к. он кратен 9, обозначим его как
3b) Вычислим значение ,
Как мы видим, мы получили, что равно произведению, один из множителей которого равен 9, а следовательно, также кратен 9 Следовательно кратность 9 справедлива и для последующих значений последовательности.
y = x³ - 3x² - 9x + 2
производная
y' = 3x² - 6x - 9
приравняем y' нулю и найдём экстремальные точки
3x² - 6x - 9 = 0
или
x² - x - 3 = 0
D = 1 + 12 = 13
√D = √13
x₁ = 0,5(1 - √13) ≈ -1,3
x₂ = 0,5(1 + √13) ≈ 2,3
Поскольку графиком производной y' = 3x² - 6x - 9 является парабола веточками вверх, то отрицательные значения производной будут находиться между корнями х₁ и х₂.
Поэтому в точке х₁ производная меняет знак с + на -. И это точка максимума.
В точке х₂ производная меняет знак с - на +, значит, это точка минимума.
ответ: в точке x₁ = 0,5(1 - √13) имеет место локальный максимум,
в точке x₂ = 0,5(1 + √13) имеет место локальный минимум
Пошаговое объяснение:
1) Определим значения выражения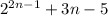
при различных значениях 
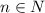как последовательность
2) Определим значения членов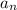
последовательности при n=1, n=2, n = 3:
3) Применим метод математической индукции.
3a) Возьмем такой член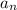
, который кратен 9 (как мы убедились выше, такое 
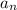существует (например, а3))
Т.к. он кратен 9, обозначим его как
3b) Вычислим значение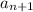
,
Как мы видим, мы получили, что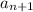
равно произведению, один из множителей которого равен 9, а следовательно, 
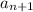также кратен 9 Следовательно кратность 9 справедлива и для последующих значений последовательности.
Что и требовалось доказать