Комбинаторные задачи. №1.В магазине "Все для чая" есть 5 разных чашек и 3 разных блюдца. Сколькими можно купить чашку с блюдцем? №2. В Стране Чудес есть три города: А, Б и В. Из города А в город Б ведет 6 дорог, а из города Б в город В - 4 дороги. Сколькими можно проехать от А до В? №3. Назовем натуральное число "симпатичным", если в его записи встречаются только нечетные цифры. Сколько существует 4-значных "симпатичных" чисел? Составить Дерево вариантов
Пошаговое объяснение:
Необходимо найти неизвестные переменные и
и 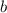 , если их сумма
, если их сумма 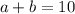 , а отношение
, а отношение 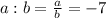 .
.
Из определения частного мы получаем, что будет равно
будет равно 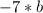 , так как чтобы найти делимое, нужно итог деления или частное умножить на делитель. Получили:
, так как чтобы найти делимое, нужно итог деления или частное умножить на делитель. Получили:  .
.
Подставим данное выражение в сумму двух переменных и найдём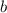 . Так как при нахождении неизвестной делитель получился отрицательным, то при делении мы имеем право минус вынести за дробь:
. Так как при нахождении неизвестной делитель получился отрицательным, то при делении мы имеем право минус вынести за дробь:
Нашли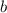 , поэтому данное значение в любое из выражений, найдем
, поэтому данное значение в любое из выражений, найдем  . Подставим во второе:
. Подставим во второе:
Сделаем проверку:
7. Мамины бусы состоят из 10 красных и 10 синих бусин в каком-то порядке.
Докажите, что в бусах есть 10 подряд бусин, среди которых поровну синих и
красных.
8. В других маминых бусах есть черные и белые бусины, причем и тех, и других
- четное количество. Обязательно ли эти бусы можно разрезать так, что в
каждой части будет ровно половина черных бусин и ровно половина белых?
9. В ряд сидят 15 мальчиков и 15 девочек. ( a ) Всегда ли из них можно выбрать
10 школьников подряд, чтобы среди них мальчиков и девочек было поровну?
( b ) Всегда ли из них можно выбрать 20 школьников подряд, среди которых
мальчиков и девочек поровну?
Пошаговое объяснение:
7. Мамины бусы состоят из 10 красных и 10 синих бусин в каком-то порядке.
Докажите, что в бусах есть 10 подряд бусин, среди которых поровну синих и
красных.
8. В других маминых бусах есть черные и белые бусины, причем и тех, и других
- четное количество. Обязательно ли эти бусы можно разрезать так, что в
каждой части будет ровно половина черных бусин и ровно половина белых?
9. В ряд сидят 15 мальчиков и 15 девочек. ( a ) Всегда ли из них можно выбрать
10 школьников подряд, чтобы среди них мальчиков и девочек было поровну?
( b ) Всегда ли из них можно выбрать 20 школьников подряд, среди которых
мальчиков и девочек поровну?