x²+(a-1)x+a²-1,5=0
Сумма квадратов корней - это х1²+х2².
Чтобы выражение имело корни, его дискриминант должен быть больше или равен 0.
D=(а-1)²-4(а²-1,5)=а²-2а+1-4а²+6=-3а²-2а+7≥0
D1=4+84=88
а1=(-1-√22)/3
а2=(-1+√22)/3
а∈((-1-√22)/3; (-1+√22)/3)
По теореме Виета:
x1+x2=1-а
x1*x2=а²-1,5
Теперь определим сумму квадратов корней:
x1²+x2²=(x1+x2)²-2x1*x2=(1-а)²-2(а²-1,5)=1-2а+а²-2а²+3=-а²-2а+4
Чтобы найти максимальное значение -а²-2а+4, нужно определить производную функции f(а)=-а²-2а+4
f`(а)=-2а-2=0
-2а=2
а=-1
На промежутке это выглядит так:
+ -
(-1)>
Это и будет точка максимума.
f(-1)=-1+2+4=5
Итак, при а=-1 сумма квадратов корней будет наибольшей.
ответ: а=-1.
Пошаговое объяснение:
( sin(x) + cos(x))^2 = 1-sin(x) * cos(x)
разложим уравнение используя (a+b)^ = a^2-ab+b^2
sin(x)^2+2sin(x)cos(x)+cos(x)^2 = 1-sin x * cos x
упрощаем выражение, используя sin(t)^2+cos(t)^2=1
1+2sin(x)cos(x) = 1-sin(x)cos(x)
упрощаем выражение, используя 2sin(t)cos(t)=sin(2t)
1+sin(2x) = 1-sin(x)cos(x)
сократим равные члены в обеих частях уравнения
sin(2x) = -sin(x)cos(x)
переместив выражение в левую часть, прибавляем противоположное ему выражение к обеим частям
sin(2x)+sin(x)cos(x) = -sin(x)cos(x)+sin(x)cos(x)
сумма двух противоположных чисел равна 0
sin(2x)+sin(x)cos(x) = 0
используем sin(2t) = 2sin(t)cos(t)
2sin(x)cos(x)+sin(x)cos(x) = 0
приводим подобные члены
3sin(x)cos(x) = 0
делим обе стороны на 3
sin(x)cos(x) = 0
если произведение равно 0, то как минимум один из множителей равен 0
sin(x) = 0
cos(x) = 0
решаем уравнение относительно х
x = kπ, k∈Z
x = +kπ, k∈Z
Объединяем
x = , k∈Z
x²+(a-1)x+a²-1,5=0
Сумма квадратов корней - это х1²+х2².
Чтобы выражение имело корни, его дискриминант должен быть больше или равен 0.
D=(а-1)²-4(а²-1,5)=а²-2а+1-4а²+6=-3а²-2а+7≥0
D1=4+84=88
а1=(-1-√22)/3
а2=(-1+√22)/3
а∈((-1-√22)/3; (-1+√22)/3)
По теореме Виета:
x1+x2=1-а
x1*x2=а²-1,5
Теперь определим сумму квадратов корней:
x1²+x2²=(x1+x2)²-2x1*x2=(1-а)²-2(а²-1,5)=1-2а+а²-2а²+3=-а²-2а+4
Чтобы найти максимальное значение -а²-2а+4, нужно определить производную функции f(а)=-а²-2а+4
f`(а)=-2а-2=0
-2а=2
а=-1
На промежутке это выглядит так:
+ -
(-1)>
Это и будет точка максимума.
f(-1)=-1+2+4=5
Итак, при а=-1 сумма квадратов корней будет наибольшей.
ответ: а=-1.
Пошаговое объяснение:
( sin(x) + cos(x))^2 = 1-sin(x) * cos(x)
разложим уравнение используя (a+b)^ = a^2-ab+b^2
sin(x)^2+2sin(x)cos(x)+cos(x)^2 = 1-sin x * cos x
упрощаем выражение, используя sin(t)^2+cos(t)^2=1
1+2sin(x)cos(x) = 1-sin(x)cos(x)
упрощаем выражение, используя 2sin(t)cos(t)=sin(2t)
1+sin(2x) = 1-sin(x)cos(x)
сократим равные члены в обеих частях уравнения
sin(2x) = -sin(x)cos(x)
переместив выражение в левую часть, прибавляем противоположное ему выражение к обеим частям
sin(2x)+sin(x)cos(x) = -sin(x)cos(x)+sin(x)cos(x)
сумма двух противоположных чисел равна 0
sin(2x)+sin(x)cos(x) = 0
используем sin(2t) = 2sin(t)cos(t)
2sin(x)cos(x)+sin(x)cos(x) = 0
приводим подобные члены
3sin(x)cos(x) = 0
делим обе стороны на 3
sin(x)cos(x) = 0
если произведение равно 0, то как минимум один из множителей равен 0
sin(x) = 0
cos(x) = 0
решаем уравнение относительно х
x = kπ, k∈Z
x =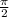 +kπ, k∈Z
+kπ, k∈Z
Объединяем
x =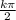 , k∈Z
, k∈Z