Координаты точки M(x, y) удовлетворяют равенству 2х+4, 5y-2кореньx-3кореньy+1= 0. Найдите tgа, где а- угол, образуемый вектором OM с положительным направлением оси ох.
Есть 5 цифр и есть 5 "мест" для них. На первое "место" можно поставить какую-то из 5и цифр. Тогда на 2ое остается 4 цифры(так как повторного использования цифр в числе по условию задачи быть не может) и т.д. вплоть до 5ого места, на которое можно поставить лишь одну цифру. Тогда всего вариантов чисел будет 5*4*3*2*1=120. И это было бы так, если бы все цифры были различными, но у нас 2 тройки, поэтому ответом на задание будет 120/2!=60 вариантов. Задача могла быть решена и немного другим У нас есть 5 мест, причем 2 из них должны быть заняты тройками. Всего вариантов расположения этих троек 5!/(3!*2!)=10. В каждом из этих вариантов остаётся 3 цифры на 3ех местах, причем их расположения 3!. Тогда количество вариантов чисел равно 10*3!=60 ответ: 60 чисел
При вращении прямоугольного треугольника ABC вокруг прямой, содержащей гипотенузу AB получается тело вращения, образованной двумя конусами с общим основанием и образующими, равными катетам треугольника AC и BC. Радиус основания конусов R равен высоте CH треугольника ABC, проведенной из вершины прямого угла C.
В ΔABC ∠C = 90°, катет AC = 4 см, катет BC = 3 см. По т.Пифагора найдем гипотенузу AB:
AB = (см).
Найдем высоту CH в ΔABC.
Воспользуемся определением синуса угла в прямоугольном треугольнике: синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе.
В ΔAHC: sin∠A = ;
В ΔABC: sin∠A = ;
; ;
Радиус основания конусов R = CH = 2,4 см.
Боковая поверхность конуса равна половине произведения длины окружности основания на образующую. S = * 2πR *L = πRL.
Боковая поверхность тела вращения равна сумме боковых поверхностей обоих конусов.
Боковая поверхность тела вращения S = 16,8π см².
Пошаговое объяснение:
Рисунок прилагается.
При вращении прямоугольного треугольника ABC вокруг прямой, содержащей гипотенузу AB получается тело вращения, образованной двумя конусами с общим основанием и образующими, равными катетам треугольника AC и BC. Радиус основания конусов R равен высоте CH треугольника ABC, проведенной из вершины прямого угла C.
В ΔABC ∠C = 90°, катет AC = 4 см, катет BC = 3 см. По т.Пифагора найдем гипотенузу AB:
AB =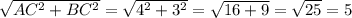 (см).
(см).
Найдем высоту CH в ΔABC.
Воспользуемся определением синуса угла в прямоугольном треугольнике: синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе.
В ΔAHC: sin∠A =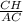 ;
;
В ΔABC: sin∠A =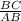 ;
;
Радиус основания конусов R = CH = 2,4 см.
Боковая поверхность конуса равна половине произведения длины окружности основания на образующую. S =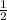 * 2πR *L = πRL.
* 2πR *L = πRL.
Боковая поверхность тела вращения равна сумме боковых поверхностей обоих конусов.
S₁ = π * 2,4 см * 4 см = 9,6π см²;
S₂ = π * 2,4 см * 3 см = 7,2π см²;
S = S₁ + S₂ = 16,8π см².