Все множество допустимых значений х определяется неравенством х >2. Чтобы среди всех этих значений найти корни уравнения, возведем обе его части в квадрат и получим:
(-x)²= x-2
(-x)²- x+2=0
Поскольку (-х)²=х², получим:
х²-х+2=0
D=b²-4ac
D=(-1)²-4·1·2=1-8= -7
Если дискриминант меньше нуля, то уравнение не может иметь корней.
√х-2=-х
Все множество допустимых значений х определяется неравенством х >2. Чтобы среди всех этих значений найти корни уравнения, возведем обе его части в квадрат и получим:
(-x)²= x-2
(-x)²- x+2=0
Поскольку (-х)²=х², получим:
х²-х+2=0
D=b²-4ac
D=(-1)²-4·1·2=1-8= -7
Если дискриминант меньше нуля, то уравнение не может иметь корней.
Поэтому уравнение √х-2=-х не имеет корней.
ответ: нет корней.
Пошаговое объяснение: 1) Возводим обе части в квадрат:
x-2=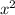
2) Переносим все на одну сторону и делим на -1:
x²-x+2=0
3) Находим дискриминант: D=b²-4ac=1-8=-7 - дискриминант отрицательный.
4. При отрицательном дискриминанте корней нет, соответственно, ответ: нет корней.