Якщо площа прямокутника АВСД=180 і ВС=20, то СД=180/20=9
Відстань від точки до прямої є перпендикуляр, опущений до прямої з точки
Тому відстань від S до прямих СД та СА є пряма SД, бо вона є перпендикулярна до площини основи → перпендикулярна до двох прямих, що перетинаються. Тому відстань до СД та СА =12см
Відстанню до ВС з точки S є відрізок SС, за теоремою трьох перпендикулярах SС перпендикулярна ВС
З △SДС за теоремою Піфагора SС^2=SД^2+ДС^2=144+81=225
Если от первых двух членов арифметической прогрессии вычесть соответственно 5 и 4, а третий член третий член оставить без изменений, то получим три первых члена геометрической прогрессии. Найти произведение этих трех членов этой арифметической прогрессии, если их сумма равна 30.
Решение
- первый член данной арифметической прогрессии.
- второй член этой прогрессии.
- третий её член
1) По условию их сумма равна 30.
это первое уравнение.
2) Согласно условию получим три члена геометрической прогрессии:
- первый член геометрической прогрессии
=>
- второй член геометрической прогрессии
- третий член геометрической прогрессии
знаменатель прогрессии;
- знаменатель прогрессии;
3)
1) =>
- первые три члена данной арифметической прогрессии
- произведение этих трех членов (вариант I )
2) =>
- первые три члена данной арифметической прогрессии
Відповідь:
Покрокове пояснення:
Якщо площа прямокутника АВСД=180 і ВС=20, то СД=180/20=9
Відстань від точки до прямої є перпендикуляр, опущений до прямої з точки
Тому відстань від S до прямих СД та СА є пряма SД, бо вона є перпендикулярна до площини основи → перпендикулярна до двох прямих, що перетинаються. Тому відстань до СД та СА =12см
Відстанню до ВС з точки S є відрізок SС, за теоремою трьох перпендикулярах SС перпендикулярна ВС
З △SДС за теоремою Піфагора SС^2=SД^2+ДС^2=144+81=225
SС=15
Аналогічно SА є відстанню до сторони АВ
З△SДА → SА^2=SД^2+ДА^2=144+400=544
SА=√(544)= 23.324
Если от первых двух членов арифметической прогрессии вычесть соответственно 5 и 4, а третий член третий член оставить без изменений, то получим три первых члена геометрической прогрессии. Найти произведение этих трех членов этой арифметической прогрессии, если их сумма равна 30.
Решение
1) По условию их сумма равна 30.
2) Согласно условию получим три члена геометрической прогрессии:
3)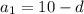
1) =>
=> 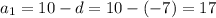
2)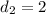 =>
=> 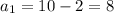
ответ: 510
960