нам дано двузначное число ab, которое при делении на 9 дает остаток 3, то есть его можно записать как
или
то есть, если из нашего двузначного числа вычесть 3, то оно будет делится на 9.
Признак делимости на 9:
Если сумма цифр делится на 9, то и само число делится на 9.
Так как по условию ab не делится на 9, то a+b не делится на 9
Но a+b-3 делится на 9. Вот только -3 не является цифрой!
Если у нас есть число a+b-3, которое кратно 9-и, то следующее кратное ему будет на 9 больше, то есть a+b-3+9=a+b+6.
Значит искомое трехзначное число:
Например, у нас есть число 39, которое дает остаток 3 при делении на 9, а число 39-3=36 делится нацело на 9. Также 3+9=12 не делится на 9, а 3+9-3=9 делится. Следующее число, после 9, которое тоже делится на 9 - это 18, то есть 9+9. Значит искомое 3-х значное число 396. 3+9+6=18, что кратно 9-и)
пусть х-ширина, а у-длина, тогда ху- площадь. составим систему
(х+4)(у-2)=ху+8 ху-2х+4у-8=ху+8 -2х+4у=8+8
(х-3)(у+1)=ху-23⇔ ху+х-3у-3=ху-23⇔ х-3у=-23+3⇔
-2х+4у=16 -2х+4у=16
х-3у=-20 обе части уравнения умножаем на 2 ⇔ 2х-6у=-40⇔
-2у=-24
у=12-длина
х=16- ширина
с=6
Пошаговое объяснение:
нам дано двузначное число ab, которое при делении на 9 дает остаток 3, то есть его можно записать как
то есть, если из нашего двузначного числа вычесть 3, то оно будет делится на 9.
Признак делимости на 9:
Если сумма цифр делится на 9, то и само число делится на 9.
Так как по условию ab не делится на 9, то a+b не делится на 9
Но a+b-3 делится на 9. Вот только -3 не является цифрой!
Если у нас есть число a+b-3, которое кратно 9-и, то следующее кратное ему будет на 9 больше, то есть a+b-3+9=a+b+6.
Значит искомое трехзначное число: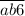
Например, у нас есть число 39, которое дает остаток 3 при делении на 9, а число 39-3=36 делится нацело на 9. Также 3+9=12 не делится на 9, а 3+9-3=9 делится. Следующее число, после 9, которое тоже делится на 9 - это 18, то есть 9+9. Значит искомое 3-х значное число 396. 3+9+6=18, что кратно 9-и)