Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
vlados546712
14.10.2021 21:26 •
Математика
Lim(4/(1-x^4))-(2/(1-x^2))=бесконечность делить на - бесконечность x стремится к 1
Показать ответ
Ответ:
kira10451
08.06.2020 01:34
ответ:
Пошаговое объяснение:
0,0
(0 оценок)
Популярные вопросы: Математика
artemvershinin
20.09.2020 12:39
При п.пт. А (-2;3)--- т. В (-3;5)т. С (4;-3) -- т. Д (x;y)Знайти: коор-ти x ,y ...
СвятаяSaints
20.09.2020 12:39
Решите уравнение-7 1/4/х = 9 2/3 / 3 1/3...
Івасічка
06.11.2022 10:08
В оранжереї є квіти 10 сортів. Скількома можна скласти букет із 15 квіток !...
sashak73
21.04.2021 13:58
Где д.з сфотайте столбиком...
shlykhta95
22.05.2022 00:31
Иследовать квадратный трехчлен f(x)=x^2-6x+12 ещё и график надо...
akink2017
22.05.2022 00:31
А)3 целых ⅜ -(а)=4.2 надо узнать не известное б)-(-⅗)=-(-4.06) ц) 3.7-(ц)=9.8. д) д+ (-6.75)=7...
alisakim2
23.10.2022 12:53
Найдите площадь квадрата периметр якого доривнюе 28 варианты ответов: а) 14 б)49 в)28 г)21...
vmyasnikova
22.01.2023 13:24
Решите уравниние протценты : Найдите а)1%; б) 30%; в)50%; г)100% от 25 га земли?...
kuzal
17.08.2021 08:32
-(а-б)-б Объясните как решать плс...
кот932
09.07.2020 08:18
Знайдіть невідомі сторони прямокутного трикутника, якщо : ˂ С = 90 ֯ , АС = 6см НУЖНО...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
ответ: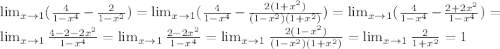
Пошаговое объяснение: