Так как АВСD - параллелограмм по условию, то его противоположные стороны равны, т.е ВС = АD = 10 м. И DЕ по условию является высотой, проведенной к стороне ВС
S(АВСD) = ВC * DЕ = 10 * 8 = 80 м²
ответ: 80 м²
№ 16
В параллелограмме АВСD биссектриса ∠ D пересекает сторону ВС в точке К. Если ∠ ВКD = 105°, ВК = 4 см, КС = 6 см, то найдите:
а) периметр
b) углы
с) площадь параллелограмма
Решение
Так как противоположные стороны параллелограмма параллельны, то углы ∠ВКD и ∠ADК являются односторонними при ВС║AD и секущей КD , ⇒ ∠ВКD + ∠ADК = 180° , ⇒ ∠ADК = 180° - 105° = 75°
Т.к. КD биссектриса по условию, то ∠ADК = ∠КDС = 75°, а ∠АDС = 2*75° = 150°.
Рассмотрим Δ КDC Он - равнобедренный, так как ∠ADК = ∠КDС являются углами при его основании КD, ⇒ равенство боковых сторон КС = DС = 6 см. Так как сумма углов тр-ка равна 180°, то ∠КСD = 180° - 75° -75° = 30°
Опустим от вершины А параллелограмма АВСD высоту АЕ на продолжение стороны СD . В полученном Δ АDЕ ∠АDЕ = 180° - ∠АDС = 180° - 150° = 30° ( так как эти углы смежные)
В Δ АDЕ по построению АЕ является катетом. Так как он лежит против угла в 30°, то будет равен половине гипотенузы АD. АD = ВС -- как противоположные стороны параллелограмма. ВС= ВК + КС = 4 + 6 = 10 см; ⇒ АD = 10 см; АЕ = 1/2 АD = 10/2 = 5 см
Пошаговое объяснение:
№15
Дано: АВСD - параллелограмм
DЕ ⊥ВC; DЕ = 8м; DK⊥AC; DK = 5м
∠САD = 30°
Найти: S( АВСD)
Решение
Рассмотрим Δ АКD DК⊥AC -по условию. ⇒Δ АКD - прямоугольный, DК -катет, АD - гипотенуза. ∠CAD =30° -- по условию ⇒ DК равен половине гипотенузы АD, ⇒АD = 2DК = 2 * 5 = 10 м
Так как АВСD - параллелограмм по условию, то его противоположные стороны равны, т.е ВС = АD = 10 м. И DЕ по условию является высотой, проведенной к стороне ВС
S(АВСD) = ВC * DЕ = 10 * 8 = 80 м²
ответ: 80 м²
№ 16
В параллелограмме АВСD биссектриса ∠ D пересекает сторону ВС в точке К. Если ∠ ВКD = 105°, ВК = 4 см, КС = 6 см, то найдите:
а) периметр
b) углы
с) площадь параллелограмма
Решение
Так как противоположные стороны параллелограмма параллельны, то углы ∠ВКD и ∠ADК являются односторонними при ВС║AD и секущей КD , ⇒ ∠ВКD + ∠ADК = 180° , ⇒ ∠ADК = 180° - 105° = 75°
Т.к. КD биссектриса по условию, то ∠ADК = ∠КDС = 75°, а ∠АDС = 2*75° = 150°.
Рассмотрим Δ КDC Он - равнобедренный, так как ∠ADК = ∠КDС являются углами при его основании КD, ⇒ равенство боковых сторон КС = DС = 6 см. Так как сумма углов тр-ка равна 180°, то ∠КСD = 180° - 75° -75° = 30°
Опустим от вершины А параллелограмма АВСD высоту АЕ на продолжение стороны СD . В полученном Δ АDЕ ∠АDЕ = 180° - ∠АDС = 180° - 150° = 30° ( так как эти углы смежные)
В Δ АDЕ по построению АЕ является катетом. Так как он лежит против угла в 30°, то будет равен половине гипотенузы АD. АD = ВС -- как противоположные стороны параллелограмма. ВС= ВК + КС = 4 + 6 = 10 см; ⇒ АD = 10 см; АЕ = 1/2 АD = 10/2 = 5 см
а)Р(АВСD) = 2*ВС + 2*DС = 2*10 +2*6 = 32 см
б) противоположные углы параллелограмма равны
∠А = ∠С = 30°
∠В = ∠D = 150°
в) S(АВСD) = АЕ * DС = 5 * 6 = 30 см²
ответ: а) 32 см; b) 30° и 150°; с) 30 см²
1.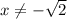 и x≤−1 и
и x≤−1 и 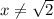 и x≥1
и x≥1
2. x=0
Пошаговое объяснение:
Заменим 2²⁻ˣ² -1 = y и приравняем к 0
3/y² - 4/y+1=0 (грубо говоря, умножим обе части на y² и получаем квадратное уравнение)
y²-4y+3=0 D=4 y₁=1 y₂=3
подставляем y₁ 2²⁻ˣ² -1 = 1 2²⁻ˣ²= 2 => 2-x²=1 x²=1 т.е. x₁= -1 x₂= 1
подставляем y₂ 2²⁻ˣ² -1 = 3 2²⁻ˣ²=2² => 2-x²=2 x²=0 т.е. x₃= 0
Так же обращаем внимание, что 2²⁻ˣ² -1 не может быть равен 0 т.е.
2²⁻ˣ² -1≠0 2²⁻ˣ² ≠ 2⁰ => 2-x²≠0 x²≠2 т.е.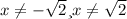
Все собираем в кучу и получаем то что в ответе