Пошаговое объяснение:
по первому замечательному пределу
sinx ≈ x
sin²x ≈ x²
и по тригонометрии
ctg²x = cos²x/sin²x
и вот имеем предел
и снова первый замечательный , это применим к дроби
тогда
и снова первый замечательный sin²(x/2) ≈ x²/2
и пришли мы, наконец, к завершению
ответ
Пошаговое объяснение:
по первому замечательному пределу
sinx ≈ x
sin²x ≈ x²
и по тригонометрии
ctg²x = cos²x/sin²x
и вот имеем предел
и снова первый замечательный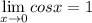 , это применим к дроби
, это применим к дроби
тогда
и снова первый замечательный sin²(x/2) ≈ x²/2
и пришли мы, наконец, к завершению
ответ