Лисенок посадил на поле два деревца — грушу и яблоню. В те дни, когда погода хорошая, груша вырастает на 30%, а яблоня — на 20%. А в те дни, когда погода
плохая, груша уменьшается на 30%, а яблоня - на 20%. Через неделю
оказалось, что одно из деревцев выросло, а другое уменьшилось. Сколько дней
была хорошая погода?

Показать ответ

Ответ:

13.11.2022 19:07

1,863 + 19,9= 21,763
15,3-6,875= 8,425

9,5 дм = 0,95 м
42,8 см = 0,428 м
7 мм= 0,007 м

4,4 дм = 0,44 м
31 см = 0,31 м
430 мм= 0,43 м
Р= 0,44+0,31+0,43= 1,18 м

1) 360 г = 0,36 кг
0,36 - 0,158 = 0,202 кг - масса второго яблока
2) 0,202+0,36= 0,562 кг - масса первого и второго яблока вместе
3) 0,85-0,562= 0,288 кг - масса третьего яблока
ответ: 0,288 кг масса третьего яблока

АВ - х см
ВС - (х-2,39) см
СД - (х + 53,2 ) см , т.к. 5,32 дм = 53,2 см
Выражение длины ломаной АВСД:
х+ (х-2,39) +(х+53,2) = х+х-2,39+х+53,2 = 3х+ 50,81
ответ: (3х+50,81 ) см

0,0(0 оценок)

Ответ:

Dashaaleshenko

11.09.2020 01:13

ДАНО

Y = (x² + 9)/x

ИССЛЕДОВАНИЕ
1. Область определения. Деление на ноль в знаменателе.
Х≠ 1.
Х∈(-∞;0)∪(0;+∞)
2. Вертикальная асимптота: Х= 1.
3. Пересечение с осью Х. Y(x) = 0 - нет.
4. Пересечение с осью У - нет
5. Наклонная асимптота
k = lim(+∞)Y(x)/x = 4*x/x = 4. Уравнение асимптоты: Y = 4*x.

6. Проверка на чётность.
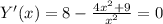
Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x)
Функция ни четная ни нечетная.
7. Поведение в точке разрыва.
lim(->0-) Y(x) = -∞.
lim(->0+) Y(x) = +∞
8, Первая производная.
$Y'(x)=8- \frac{4x^2+9}{x^2}=0$
6. Локальные экстремумы.
Y'(x) = 0, x1 = - 3/2, x2 = 3/2
Максимум Y(-3/2)= .-12.

Минимум Y(3/2) = 12.
7. Участки монотонности функции.
Возрастает - Х∈(-∞;-3/2]∪[3/2;+∞).

Убывает - Х∈[-3/2;0)∪(0;3/2]
8. Вторая производная.

$Y"(x)=- \frac{8}{x}+ \frac{8*x^2+18}{x^3} =0$

Корней нет. Точек перегиба (на графике) - нет.
9. Выпуклая - "горка" - Х∈(-∞;0). Вогнутая - "ложка" - Х∈(0;+∞)