Оскільки лицар не може кинути туди 0 монет, бо за умовою він кидає від 1 до 10, то кількість монет завжди змінюється. Подивимося, які числа в межах 100 діляться на 25. Це 25, 50, 75, 100. А на 22: 22,44,66,88.
Кількість монет не може ділитися завжди на 22, бо тоді йому б прийшлося кожного разу додавати 22 монети.
З цієї ж причини не може бути кожного разу 25, бо 25 не може він додавати за умовою.
Нехай спочатку було 25 монет. Щоб число ділилося на 22. він має додати 44-25=19 монет, тому ця ситуація не підходить, бо максимальна кількість 10 монет.
Розглянемо випадок, коли спочатку було число 22, тоді воно ділиться на 22, потім кидає 3 монети, і число ділиться на 25. Здавалося б, що він міг і не помилятися, але візьмемо інше число, яке ділиться на 22, наприклад 88, тоді наступного разу число має ділитися на 25, тобто наступне число 100. Знайдемо різницю між 100 і 88, 100-88=12, а 12 більше, ніж максимальна кількість монет, яку міг закинути чоловік.
Смысл задания в том, чтобы разложить данное выражение на множители. Сделать это можно двумя
1-ый
Понятно, что увидеть это достаточно сложно, поэтому не каждый может пользоваться таким приемом. Для тех, кто не может пользоваться таким методом, есть более длинный, но универсальный алгоритм.
2-ой
Решим данное уравнение относительно a:
Несложно увидеть здесь квадратное уравнение.
Значит решаем через дискриминант:
Теперь воспользуемся формулой разложения квадратного трехчлена на множители:
Пришли к тому же результату. Я рекомендую пользоваться вторым
Теперь несложно получить ответ, если вспомнить, что произведение равно 0, если хотя бы один из его множителей равен 0, а другой при этом не теряет смысла.
Відповідь:
Покрокове пояснення:
Оскільки лицар не може кинути туди 0 монет, бо за умовою він кидає від 1 до 10, то кількість монет завжди змінюється. Подивимося, які числа в межах 100 діляться на 25. Це 25, 50, 75, 100. А на 22: 22,44,66,88.
Кількість монет не може ділитися завжди на 22, бо тоді йому б прийшлося кожного разу додавати 22 монети.
З цієї ж причини не може бути кожного разу 25, бо 25 не може він додавати за умовою.
Нехай спочатку було 25 монет. Щоб число ділилося на 22. він має додати 44-25=19 монет, тому ця ситуація не підходить, бо максимальна кількість 10 монет.
Розглянемо випадок, коли спочатку було число 22, тоді воно ділиться на 22, потім кидає 3 монети, і число ділиться на 25. Здавалося б, що він міг і не помилятися, але візьмемо інше число, яке ділиться на 22, наприклад 88, тоді наступного разу число має ділитися на 25, тобто наступне число 100. Знайдемо різницю між 100 і 88, 100-88=12, а 12 більше, ніж максимальна кількість монет, яку міг закинути чоловік.
Тому він помилявся!
(см. объяснение)
Пошаговое объяснение:
Смысл задания в том, чтобы разложить данное выражение на множители. Сделать это можно двумя
1-ый
Понятно, что увидеть это достаточно сложно, поэтому не каждый может пользоваться таким приемом. Для тех, кто не может пользоваться таким методом, есть более длинный, но универсальный алгоритм.
2-ой
Решим данное уравнение относительно a:
Несложно увидеть здесь квадратное уравнение.
Значит решаем через дискриминант:
Теперь воспользуемся формулой разложения квадратного трехчлена на множители:
Пришли к тому же результату. Я рекомендую пользоваться вторым
Теперь несложно получить ответ, если вспомнить, что произведение равно 0, если хотя бы один из его множителей равен 0, а другой при этом не теряет смысла.
Значит:
или
Откуда получаем, что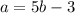 или
или 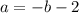 .
.
Задание выполнено!