Поскольку Маша не может выговорить буквы М и Ш, она не сумеет произнести числа, содержащие в себе цифры 7 (сеМь), 8 (восеМь), и 6 (Шесть).
То есть, чтобы понять, сколько чисел от 1 до 1000 она сможет правильно произнести, нужно понять, сколько однозначных, двузначных и трехзначных чисел не содержат в своей записи цифры 6, 8 и 7.
1) Найдем, сколько таких однозначных чисел.
Раз цифр всего 10, и мы исключаем 0 (числа идут от 1), 6, 8 и 7, то есть 4 цифры, остается 6 вариантов.
2) Найдем, сколько двузначных чисел, в которых не содержится ни 6, ни 7, ни 8.
Первая цифра не может быть ни 0 (число не может начинаться с нуля), ни 6, ни 7, ни 8, — значит, 6 вариантов первой цифры.
Вторая цифра не может быть ни 6, ни 7, ни 8, — значит, 7 вариантов второй цифры.
Согласно комбинаторному правилу умножения, если объект А можно выбрать n количеством , а объект B — m количеством , то пару объектов можно выбрать .
Таким образом, вариантов двузначных чисел, не содержащих 6, 7 и 8, всего 42.
3) Рассмотрим трехзначные числа.
Первая цифра в них не может быть 0, 6, 7 или 8, — остается 6 вариантов.
Вторая цифра не может быть 6, 7, 8, — 7 вариантов.
Аналогично, существует 7 вариантов третьей цифры.
Получаем =294 варианта подходящих нам трехзначных чисел.
Суммируем варианты однозначных, двузначных и трезначных чисел от 1 до 1000, не содержащих цифр 6, 7 и 8:
Поскольку Маша не может выговорить буквы М и Ш, она не сумеет произнести числа, содержащие в себе цифры 7 (сеМь), 8 (восеМь), и 6 (Шесть).
То есть, чтобы понять, сколько чисел от 1 до 1000 она сможет правильно произнести, нужно понять, сколько однозначных, двузначных и трехзначных чисел не содержат в своей записи цифры 6, 8 и 7.
1) Найдем, сколько таких однозначных чисел.
Раз цифр всего 10, и мы исключаем 0 (числа идут от 1), 6, 8 и 7, то есть 4 цифры, остается 6 вариантов.
2) Найдем, сколько двузначных чисел, в которых не содержится ни 6, ни 7, ни 8.
Первая цифра не может быть ни 0 (число не может начинаться с нуля), ни 6, ни 7, ни 8, — значит, 6 вариантов первой цифры.
Вторая цифра не может быть ни 6, ни 7, ни 8, — значит, 7 вариантов второй цифры.
Согласно комбинаторному правилу умножения, если объект А можно выбрать n количеством , а объект B — m количеством , то пару объектов можно выбрать .
Таким образом, вариантов двузначных чисел, не содержащих 6, 7 и 8, всего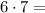
42.
3) Рассмотрим трехзначные числа.
Первая цифра в них не может быть 0, 6, 7 или 8, — остается 6 вариантов.
Вторая цифра не может быть 6, 7, 8, — 7 вариантов.
Аналогично, существует 7 вариантов третьей цифры.
Получаем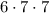
=294 варианта подходящих нам трехзначных чисел.
Суммируем варианты однозначных, двузначных и трезначных чисел от 1 до 1000, не содержащих цифр 6, 7 и 8:
ответ: 342.