Рассмотрим немного другую задачу. Выбрасываются k (k>0) кубиков, человек загадывает число от 1 до 6. Найти вероятность того, что число присутствует хотя бы на одном из кубиков
Событие А="число присутствует хотя бы на одном из кубиков" противоположно событию В="число не присутствует ни на одном из кубиков". Тогда
Вероятность не угадать число на одном кубике равна (среди 6 чисел 5 не подойдут). Тогда вероятность не угадать число на k кубиках равна - это и есть искомая вероятность в данной задаче.
Вернемся к исходной задаче. На 1ом этапе вероятность угадать число равна . При условии угадывания числа, на следующем этапе остается 6-1=5 кубиков. Тогда вероятность угадывания на 2ом этапе равна . При условии угадывания числа, на следующем этапе остается 5-1=4 кубиков. И т.д. На последнем этапе останется 2 кубика, и вероятность угадывания будет равна
1. Пусть приборов n. Тогда проводов 5n/2, так как каждый провод считается дважды. (прибор - вершина графа, провод - ребро). Следовательно, число проводов делится на 5 и поэтому не может равняться 33. 2. Станция -вершина, путь -ребро. У нас нечетное число (4+5=9) вершин, соединенных с нечетным числом вершин, чего не может быть (см 4-ю задачу) 3. Область - вершина, ребро между вершинами - если области имеют общую границу. 1, 3 и 5 - нечетные числа, 17 -нечетное число. Далее - как в задаче 4. 4. Люди - вершины, ребра -между вершинами, которые дружат друг с другом. Суммируя числа ребер, выходящих из вершин, мы должны получившееся число поделить на два, так как каждое ребро было сосчитано дважды. Если бы число вершин, из которых выходит нечетное число ребер, было нечетно, то на два поделить не удалось бы.
Рассмотрим немного другую задачу. Выбрасываются k (k>0) кубиков, человек загадывает число от 1 до 6. Найти вероятность того, что число присутствует хотя бы на одном из кубиков
Событие А="число присутствует хотя бы на одном из кубиков" противоположно событию В="число не присутствует ни на одном из кубиков". Тогда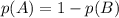
Вероятность не угадать число на одном кубике равна (среди 6 чисел 5 не подойдут). Тогда вероятность не угадать число на k кубиках равна
(среди 6 чисел 5 не подойдут). Тогда вероятность не угадать число на k кубиках равна 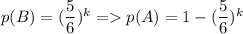 - это и есть искомая вероятность в данной задаче.
- это и есть искомая вероятность в данной задаче.
Вернемся к исходной задаче. На 1ом этапе вероятность угадать число равна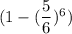 . При условии угадывания числа, на следующем этапе остается 6-1=5 кубиков. Тогда вероятность угадывания на 2ом этапе равна
. При условии угадывания числа, на следующем этапе остается 6-1=5 кубиков. Тогда вероятность угадывания на 2ом этапе равна 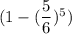 . При условии угадывания числа, на следующем этапе остается 5-1=4 кубиков. И т.д. На последнем этапе останется 2 кубика, и вероятность угадывания будет равна
. При условии угадывания числа, на следующем этапе остается 5-1=4 кубиков. И т.д. На последнем этапе останется 2 кубика, и вероятность угадывания будет равна 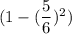
Тогда искомая вероятность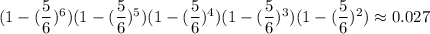
2. Станция -вершина, путь -ребро. У нас нечетное число (4+5=9) вершин, соединенных с нечетным числом вершин, чего не может быть (см 4-ю задачу)
3. Область - вершина, ребро между вершинами - если области имеют общую границу. 1, 3 и 5 - нечетные числа, 17 -нечетное число. Далее - как в задаче 4.
4. Люди - вершины, ребра -между вершинами, которые дружат друг с другом. Суммируя числа ребер, выходящих из вершин, мы должны получившееся число поделить на два, так как каждое ребро было сосчитано дважды. Если бы число вершин, из которых выходит нечетное число ребер, было нечетно, то на два поделить не удалось бы.