ответ: 152π, 1372/3 π, 196π, /5, 36/25 π
Пошаговое объяснение:
Для цилиндра:
Разделим цилиндр на прямоугольник со стороной 2πR и высотой h, и на два кружочка площадью πR^2.
S = 2*πR^2 + 2πRh = 152π см^2
Для шара:
Объем шара вычисляется по ф-ле πR^3. Значит здесь он равен π
Площадь поверхности шара определяется как 4πR^2. Здесь она равна 196π.
Для конуса:
Образующая легко находиться по теореме Пифагора как√ + . Здесь она равна .
Площадь осевого сечения находится как площадь круга πR^2. Тут она равна π
ответ: 152π, 1372/3 π, 196π,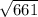
/5, 36/25 π
Пошаговое объяснение:
Для цилиндра:
Разделим цилиндр на прямоугольник со стороной 2πR и высотой h, и на два кружочка площадью πR^2.
S = 2*πR^2 + 2πRh = 152π см^2
Для шара:
Объем шара вычисляется по ф-ле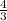
πR^3. Значит здесь он равен 
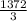π
Площадь поверхности шара определяется как 4πR^2. Здесь она равна 196π.
Для конуса:
Образующая легко находиться по теореме Пифагора как√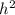
+ 
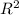. Здесь она равна 
.
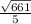Площадь осевого сечения находится как площадь круга πR^2. Тут она равна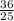
π