Математика,11кл, Задание с ЕГЭ Расстояние между пристанями A и B равно 144 км. Из A в B по течению реки отправился плот, а через 2 часа вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 3 км/ч. ответ дайте в км/ч.

Показать ответ

Ответ:

maxmax41

19.08.2020 06:18

15 км/ч

Пошаговое объяснение:

Плот плывет со скоростью реки

66 : 3 = 22 (часа) - был в пути плот

22-2 = 20 (часов) - время яхты

х км/ч - скорость яхты в стоячей воде

х+3 (км/ч) - скорость яхты по течению реки

х-3 (км/ч) - скорость яхты против течения реки

144/(х+3) + 144/(х-3) = 20

144(х-3) + 144(х+3) = 20(х+3)(х-3)

144х + 144х = 20(х²-9)

20х² - 288х - 180 = 0 - сократим все в 4 раз

5х² - 72х - 45 = 0

5х² - 75х + 3х- 45 = 0

5х(х-15) + 3(х-15) = 0

(5х+3)(х-15) = 0

Первый корень: 5х+3 = 0; 5х = -3 - результат отрицательный

Второй корень: х-15 = 0

х = 15 (км/ч) - скорость яхты в стоячей воде

0,0(0 оценок)

Ответ:

Мышастик

19.08.2020 06:18

Пошаговое объяснение:

Плот движется со скоростью течения. Следовательно, время его движения равно 66 / 3 = 22 ч. Яхта же плыла на 2 часа меньше, то есть 20 ч.

Пусть x км/ч — скорость яхты в неподвижной воде. Тогда скорость по течению равна x+3 км/ч, а против течения — x-3 км/ч. Значит, из A в B она плыла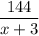 $\dfrac{144}{x+3}$ ч, а обратно — 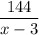$\dfrac{144}{x-3}$ ч. Суммарно:

$\dfrac{144}{x+3}+\dfrac{144}{x-3}=20|:4\\\dfrac{36}{x+3}+\dfrac{36}{x-3}=5\\\dfrac{36(x-3)+36(x+3)-5(x+3)(x-3)}{(x+3)(x-3)}=0\\\dfrac{-5x^2+72x+45}{x^2-9}=0\Leftrightarrow\displaystyle\left \{ {{5x^2-72x-45=0} \atop {x^2-9\neq 0}} \right. \left \{ {{x=-\frac{3}{5},15} \atop {x\neq \pm 3}} \right. \Rightarrow x=-\frac{3}{5},15$