неповторяющихся карточек можно выложить в ряд
При этом из этих нам подходит только один: когда буква "М" - на первом месте, "О" - на втором, ... , "А" - на шестом.
Следовательно, искомая вероятность равна .
В партии из деталей имеется стандартных и бракованных.
Если среди двух взятых на угад одна бракованная, то реализуется два сценария:
Первая - бракованная, вторая - стандартная.
Первая - стандартная, вторая - бракованная.
(В обоих случаях вероятности равны.)
Теперь мы можем посчитать искомую вероятность:
При этом из этих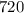 нам подходит только один: когда буква "М" - на первом месте, "О" - на втором, ... , "А" - на шестом.
нам подходит только один: когда буква "М" - на первом месте, "О" - на втором, ... , "А" - на шестом.
Следовательно, искомая вероятность равна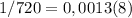 .
.
ответ:В партии из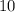 деталей имеется
деталей имеется 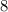 стандартных и
стандартных и 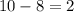 бракованных.
бракованных.
Если среди двух взятых на угад одна бракованная, то реализуется два сценария:
Первая - бракованная, вторая - стандартная.
В этом случаеПервая - стандартная, вторая - бракованная.
Здесь(В обоих случаях вероятности равны.)
Теперь мы можем посчитать искомую вероятность:
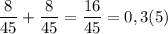
ответ:5х+х=486
6х=486
х=81 км
81:81=1ч - по автомагистрали
81*5:45=9ч - по узкой дороге
2) а)56-18:x*5+17=43
18:x*5=56+17-43
18:x*5=30
х=18:(30:5)
х=3
б)4(12-x):3+14=22
4(12-x):3=22-14
12-х=8*3:4
12-х=6
х= 6
3) 17.284.679+75.852:84*3007=17.284.679+903*3007=17.284.679+2.715.321=20.000.000
4) а)x:370=7400
х=7400*370
х=2738000
б)3216:(5y-109)=16
5у-109=3216:16
5у-109=201
5у=201+109
y=310:5
у=62
в) (10x-68):36:6=48:24
(10x-68):36:6=2
(10x-68):36=2*6
(10x-68):36=12
(10x-68)=12*36
(10x-68)=432
10х=432+68
10х=500
х=10
5) s - объем бассейна = 3888л
за час три трубы:
s/9+s/12+s/18= 432+324+216=972 л
3888:972=4 ч - три трубы заполнят бассейн