МАТЕМАТИКА В ЖИЗНИ 6 Составь выражения, найди их значения.
Айна готовится к конкурсу рисунков О космосе. Она пришла
в магазин канцтоваров и стала рассматривать ценники. По-
моги ей вычислить.
000000
000000
392 тг
490 тг
294 тг
а) Какова общая стоимость двух коробок красок, трёх набо-
ров Кисточек и четырёх палитр?
6) На сколько стоимость двух коробок красок и трёх наборов
Кисточек дороже двух палитр?
в) Во сколько раз набор кисточек дешевле пяти коробок красок?
ответ: N = 10
Т.к. в N-ичной системе счисления присутствует число 7 (и, соответственно, цифра 7), то основание системы больше 7, т.е. N > 7.
Так как 7 - простое число, то надо рассмотреть 2 случая: 1)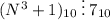 2)
2) 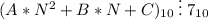 ∀ цифр A, B, C < N
∀ цифр A, B, C < N
1)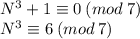
Представим N в виде x+7k, где k,x∈N∪{0}, x∈[0,6]. Подставим:
Последовательно подставляя все возможные значения x в полученное уравнение, получаем, что оно верно при x = 3, x = 5 и x = 6.
Получаем 3 серии решений: N = 3 + 7k, N = 5 + 7k, N = 6 + 7k, k∈N, откуда наименьшее N в данном случае, с учетом условия N > 7, равно 3 + 7 = 10
2) Так как утверждение должно быть верно для ∀ цифр A, B, C < N, то оно будет верно и для наборов (1, 0, 0) и (1, 0, 1).
Тогда: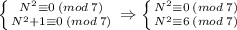
При этом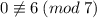 . Значит система сравнений не имеет решений. А значит не существует такого N, чтобы условие выполнялось
. Значит система сравнений не имеет решений. А значит не существует такого N, чтобы условие выполнялось
Значит и ответом будет N = 10
Исследовать функцию и построить график.
Решение:
1) Функция не определена при обращении в ноль знаменателя, т.е. x ≠ 0 .
D(f) ≡ R \ {0} ≡
2) В функции встречаются только чётные степени аргумента, а значит она чётная. Докажем это:
Найдём первую производную функции y(x) :
При x = 0, производная y'(x) – не определена, как и сама функция, при всех остальных значениях аргумента функция и её первая производная определены и конечны, а значит функция непрерывная на всей области определения D(f) – на всей числовой прямой, кроме ноля.
3) Функция не определена при x = 0 . Это точка разрыва. При этом её значение стремится к положительной бесконечности, что легко доказать:
Если приравнять функцию к нолю, получим:
Значит, никаких пересечений графика с осями координат нет.
4. Найдем асимптоты y(x).
По найденному в (3) пределу, ясно, что линия x = 0 – является вертикальной двухсторонней асимптотой графика функции y(x) .
Посмотрим, что происходит с функцией y(x) при устремлении аргумента к ±
Значит, уходя на бесконечность обоих знаков график функции y(x) имеет двунаправленную горизонтальную асимптоту y = 2 ;
Наклонных асимптот нет, и не может быть, так как есть горизонтальные с обеих сторон.
5. Первая производная функции y(x) :
Значит, функция возрастает на
Уравнение
6. Найдём вторую производную функции y(x) :
В силу общей положительности второй производной – график функции всегда «улыбается», т.е. он вогнут, или, говоря иначе: он закручивается против часовой стрелки на всём своём протяжении при проходе по числовой оси аргументов слева направо.
Поскольку выгнутость повсеместна, то и точек перегиба не может быть. И их нет, соответственно.
7.
При х = ± 1 : : : y(x) = 3 ;
При х = ± 2 : : : y(x) = 2.25 ;
При х = ± 1/2 : : : y(x) = 6 ;
Строим график: