Мати напекла 100 млинців та склала їх один на один. Вийшла башта» висотою в 47 см. Яка товщина одного млинця?

Показать ответ

Ответ:

Nastena11102003

01.06.2022 19:58

Три карточки можно расположить так :

123, 132, 213, 231, 312, 321 - 6 вариантов (n=6)

Варианты по условию

132, 312, 213, 231 - 4 варианта ( m=4 )

Вероятность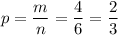 $p=\dfrac mn=\dfrac 46=\dfrac 23$

=========================================

Решение с формул

Общее количество перестановок трёх карточек

$n=P_3=3!=1\cdot 2\cdot 3=6$

Если рассматривать две находящиеся рядом нечётные карточки как единую группу, то вторым элементом останется чётная карточка.Тогда количество благоприятных вариантов есть произведение двух перестановок, общей и внутри нечётной группы

$m=P_2\cdot P_2=2!\cdot2!=4$

Вероятность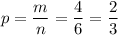 $p=\dfrac mn=\dfrac 46=\dfrac 23$

ответ : 2/3

0,0(0 оценок)

Ответ:

YTTeamGardnYT

29.07.2020 18:51

НОК (Наименьшее Общее Кратное) - двух целых чисел m и n есть наименьшее натуральное число, которое делится на m и n без остатка.

Находится следующим образом: разлагаем данные числа на простые множители выписываем все простые множители, входящие хотя бы в одно из данных чисел, каждый из взятых множителей возводим в наибольшую из тех степеней, с которыми он входит в заданные числа. Производим умножение.

В качестве примера найдем НОК (384; 540)
   384 = 2*2*2*2*2*2*2*3 = 2⁷ * 3
   540 = 2*2*3*3*3*5 = 2² * 3³ * 5
   НОК (384; 540) = 2⁷ * 3³ * 5 = 128*27*5 = 17280

0,0(0 оценок)

Популярные вопросы: Математика