Мистер фокс записал на доске число (9*15-1)^2019 . предварительно посчитав сумму цифр этого числа, мистер фокс стер число с доски и записал вместо него сумму цифр. он продолжал повторять эту операцию до тех пор, пока на доске не осталось однозначное число. какое число осталось на доске?
Пусть S(n) - сумма цифр натурального числа. Докажем, что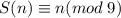
Пусть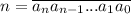 . Тогда
. Тогда
Доказано.
Тогда очевидно, что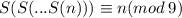 , и оставшееся в конце однозначное число дает при делении на 9 тот же остаток, что и исходное число.
, и оставшееся в конце однозначное число дает при делении на 9 тот же остаток, что и исходное число.
Единственное однозначное число, дающее остаток 8 при делении на 9, - это 8.
ответ: 8