Поменяем местами переменные и и снова выразим через (с учетом того, что ).
Таким образом, обратной функцией к данной будет функция
Изобразим графики данных функций.
Уравнение преобразуем к виду
При графиком этой функции будет правая ветка обычной параболы , смещенная на одну клетку вправо и на одну клетку вниз (на рисунке нарисован оранжевым).
График обратной функции получается из графика функции путем его смещения на одну клетку влево и одну клетку вверх (на рисунке нарисован синим).
Как несложно заметить, графики взаимообратных функций симметричны относительно прямой .
По условию АВ=6 ⇒ АС:6=2:3, АС=4 .
А )Если точка С лежит левее точки А
САВ,
В)Если точка С лежит правее точки А, то чертёж такой :
___АС___В.
Введем числовую ось ох , где точка С будет началом и значит ее координата 0, С(0).
Пусть координата произвольной точки Х(х)
А) Тогда координаты точек А , В , X следующие:
1 случай . С(0)А(4)___Х(х)В(10),
Найдем длины отрезков
ХА=|х-4|, ХВ=|10-х|, ХС=|х-0|. Всё под модульные выражения положительны, поэтому раскроются со знаком + . Подставим в условие
Х-4+10-х+х=9 , х=3 ⇒ Точка Х левее А на 1 единицу, ХА=1, ХВ=7, ХС=3
Не является решением , тк сумма длин не 9.
2 случай . С(0)__Х(х)___А(4)В(10),
Найдем длины отрезков
ХА=|4-х|, ХВ=|10-х|, ХС=|х-0|. Подставим в условие
4-х+10-х+х=9 , х=5 ⇒ Точка Х(5) правее А(4) на 1 единицу , ХА=1, ХВ=5, ХС=5 . Не является решением , тк сумма длин не 9.
В )Координаты точек А , В , Х следующие:
1 случай . __А(-4)___С(0)_Х(х)В(2),
Найдем длины отрезков
ХА=|х+4|, ХВ=|2-х|, ХС=|х-0|. Подставим в условие
Х+4+2-х+х=9 , х=3 ⇒ Точка Х(3) правее В на 1 единицу, ХА=7, ХВ=1, ХС=3. Не является решением , тк сумма длин не 9.
2 случай . ___А(-4)__Х(х)__С(0)__В(2),
Длины отрезков
ХА=|х+4|, ХВ=|2-х|, ХС=|0-х|. Подставим в условие
Х+4+2-х-х=9 , х=-3 ⇒ Точка Х(-3) правее А(-4) на 1 единицу , ХА=1, ХВ=5, ХС=3. Является решением , тк сумма длин 9.
ответ
А__Х___С__В, АХ:ХВ=1:5
Пошаговое объяснение:
Поменяем местами переменные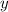 и
и  и снова выразим
и снова выразим 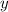 через
через  (с учетом того, что
(с учетом того, что 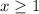 ).
).
Таким образом, обратной функцией к данной будет функция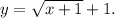
Изобразим графики данных функций.
Уравнение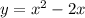 преобразуем к виду
преобразуем к виду
При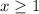 графиком этой функции будет правая ветка обычной параболы
графиком этой функции будет правая ветка обычной параболы 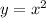 , смещенная на одну клетку вправо и на одну клетку вниз (на рисунке нарисован оранжевым).
, смещенная на одну клетку вправо и на одну клетку вниз (на рисунке нарисован оранжевым).
График обратной функции получается из графика функции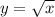 путем его смещения на одну клетку влево и одну клетку вверх (на рисунке нарисован синим).
путем его смещения на одну клетку влево и одну клетку вверх (на рисунке нарисован синим).
Как несложно заметить, графики взаимообратных функций симметричны относительно прямой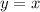 .
.