Обозначим -- первый член арифметической прогрессии и разность арифметической прогрессии соответственно (то есть, разность между соседними элементами пусть равна ). Тогда второй член последовательности равен
а седьмой равен
По условию мы знаем, что подставляя выражения для и получаем такое уравнение:
Итак, теперь разность мы знаем. Воспользуемся условием, что третий член равен 9:
с одной стороны
(так как d = 4)
с другой
Значит
,
то есть
Пусть нам надо взять членов, чтобы получить сумму
.
По формуле, сумма арифметической прогрессии равна
что с учетом превращается в
Так как то нам надо решить квадратное уравнение
Решая это уравнение по формуле дискриминанта, получаем 2 решения:
Внимание, расшифровываю
Пошаговое объяснение:
Обозначим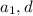 -- первый член арифметической прогрессии и разность арифметической прогрессии соответственно (то есть, разность между соседними элементами пусть равна
-- первый член арифметической прогрессии и разность арифметической прогрессии соответственно (то есть, разность между соседними элементами пусть равна 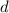 ). Тогда второй член последовательности равен
). Тогда второй член последовательности равен
а седьмой равен
По условию мы знаем, что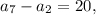 подставляя выражения для
подставляя выражения для 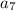 и
и 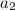 получаем такое уравнение:
получаем такое уравнение:
Итак, теперь разность мы знаем. Воспользуемся условием, что третий член равен 9:
с одной стороны
с другой
Значит
то есть
Пусть нам надо взять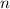 членов, чтобы получить сумму
членов, чтобы получить сумму
По формуле, сумма арифметической прогрессии равна
Так как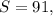 то нам надо решить квадратное уравнение
то нам надо решить квадратное уравнение
Решая это уравнение по формуле дискриминанта, получаем 2 решения:
Формула п-го члена арифметической прогрессии равна:
an=a1+d(n-1)
an-n -ый член прогрессии
а1- первый член прогрессии
d- разность прогрессии ( смотри теорию в учебнике или г)
тогда седьмой член прогрессии из выше написанной формулы находим
а7=а1+6d
второй член а2=а1+d
третий a3=a1+2d
Все эти формулы есть в твоем решении посмотри
Далее согласно условия:a3=a1+2d=9
разница а7-а2=20, то есть (а1+6d)-(а1+d)=20
а1+6d-а1-d=20
5d=20 отсюда d=20/5=4
теперь из формулы
a3=a1+2d=9
a1+2*4=9
а1=9-8=1
Формула суммы n членов арифметической прогрессии равна
S=(2a1+d(n-1))2*)n
91=((2*1+4n-4)/2)*n
91=(2n-1)*n
2n^2-n-91=0
решаем квадратное уравнение через дискриминант
D=b^2-4ac=1+4*2*91=729
n1 =(-b-√D)/2a=(1-27)/4=-26/4 (не подходит по условию)
n2 =(-b+√D)/2a=(1+27)/4=28/4=7
ответ n=7
Пошаговое объяснение: