Моро р/т стр 45 первая часть номер ( )

0

Пошаговое объяснение:

Один корень х=а

Решаем уравнение  5х-x^2-5=1 (тогда второй сомножитель равен 0).

x^2-5x=-6

x^2-5x+6,25=0,25

(x-2,5)^2=0,5^2

x1=3 x2=2

чтобы различных решений было ровно 2 нужно, чтобы а совпадал со значением одного из корней. Это а=3 и а=2.

Сумма значений 3+2=5

Если же условие такое, что уравнение имеет хотя бы два различных корня, то а - любое из указанного множества.

И решений может быть 3.

Однако, при этом выражение для аргумента логарифма   должно быть положительным. Если х=а и а меньше либо равно 0 -выражение не имеет смысла. То же при х=1,х=4, х=5 и х=6. Значит при всех а кроме 2 и 3  значение х=а нея является решением и корней ровно 2.

Знчит при любом а корнеей  два и сумма значений а в облсти (-6,6) равна 0.

AC = 2√3, BC = 2√6, BN = 3√3

Пошаговое объяснение:

Пусть третья медиана — BN, точка пересечения медиан — O.

Проведём KM₁ || CM. ∠AOM = ∠AKM₁ = 90°, ∠AMO = ∠AM₁K как соответственные ⇒ ΔAOM и ΔAKM₁ подобны ⇒ AM : AM₁ = AO : AK = 2 : 3 (по свойству медиан) ⇒ OM : KM₁ = 2 : 3.

CM — медиана, проведённая из прямого угла, CM = AB/2 = 3. CO : OM = 2 : 1 ⇒ OM = 2CM/3 = 1 ⇒ KM₁ = 3OM/2 = 3/2.

KM₁ || CM, CK = KB ⇒ MM₁ = M₁B = (AB/2) / 2 = AB/4. Тогда AM₁ = AM + MM₁ = AB/2 + AB/4 = 3AB/4 = 9/2. ΔAKM₁ — прямоугольный ⇒ .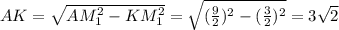

AO : OK = 2 : 1 ⇒ AO = 2√2, CO : OM = 2 : 1 ⇒ CO = 2. ΔAOC — прямоугольный ⇒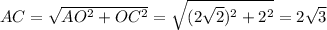 . Тогда , .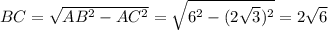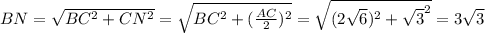